
分析 (1)先求出基本事件总数,再求出甲、乙两班选择不同曲目包含的基本事件个数,由此能求出甲、乙两班选择不同曲目的概率.
(2)由已知X的可能取值为1,2,3,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(1)在我校自编操比赛中,甲班、乙班、丙班、丁班均可从A、B、C三首不同曲目中任选一首,
∴甲、乙两班选择不同曲目的概率P=$\frac{{A}_{3}^{2}}{{3}^{2}}$=$\frac{2}{3}$.
∴甲、乙两班选择不同曲目的概率为$\frac{2}{3}$.
(2)∵这四个班级总共选取了X首曲目,∴X的可能取值为1,2,3,
P(X=1)=$\frac{3}{{3}^{4}}$=$\frac{1}{27}$,
P(X=2)=$\frac{{C}_{3}^{2}({2}^{4}-2)}{{3}^{4}}$=$\frac{14}{27}$,
P(X=3)=$\frac{{C}_{3}^{1}{C}_{4}^{2}{C}_{2}^{1}}{{3}^{4}}$=$\frac{12}{27}$.
∴X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{27}$ | $\frac{14}{27}$ | $\frac{12}{27}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 序号 | 分组(分数段) | 频数(人数) | 频率 |
| 1 | [60,70) | 8 | 0.16 |
| 2 | [70,80) | 22 | a |
| 3 | [80,90) | 14 | 0.28 |
| 4 | [90,100) | b | c |
| 合计 | d | 1 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 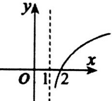 | B. |  | C. | 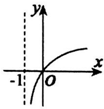 | D. | 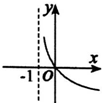 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
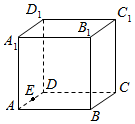 如图,棱长为2的正方体ABCD-A1B1C1D1,E为棱AD的中点,则经过点B1、D1和E三点的截面的左视图的面积为( )
如图,棱长为2的正方体ABCD-A1B1C1D1,E为棱AD的中点,则经过点B1、D1和E三点的截面的左视图的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com