
分析 (1)设圆心的坐标为(x,y),由题意可得$\sqrt{{x}^{2}+(y-\frac{1}{2})^{2}}$=$\sqrt{{y}^{2}+\frac{1}{4}}$,两边平方化简即可得到轨迹方程;
(2)可知A(-$\sqrt{a}$,a),B($\sqrt{a}$,a),设C(m,m2),由该抛物线上存在点C,使得∠ACB为直角,可得$\overrightarrow{AC}$•$\overrightarrow{BC}$=0.即可得到a的取值范围;
(3)设AF=a,BF=b,由抛物线定义,2MN=a+b.再由余弦定理可得|AB|2=a2+b2-2abcos120°,进而根据a+b≥2$\sqrt{ab}$,求得|AB|的范围,进而可得答案.
解答  解:(1)设圆心的坐标为(x,y),由题意可得
解:(1)设圆心的坐标为(x,y),由题意可得
$\sqrt{{x}^{2}+(y-\frac{1}{2})^{2}}$=$\sqrt{{y}^{2}+\frac{1}{4}}$,
化简可得,y=x2,
即为动圆圆心的轨迹L的方程;
(2)如图所示,可知A(-$\sqrt{a}$,a),B($\sqrt{a}$,a),
设C(m,m2),$\overrightarrow{AC}$=(m+$\sqrt{a}$,m2-a),$\overrightarrow{BC}$=(m-$\sqrt{a}$,m2-a).
∵该抛物线上存在点C,使得∠ACB为直角,
∴$\overrightarrow{AC}$•$\overrightarrow{BC}$=(m+$\sqrt{a}$)(m-$\sqrt{a}$)+(m2-a)2=0.
化为m2-a+(m2-a)2=0.
∵m≠±$\sqrt{a}$,∴m2=a-1≥0,解得a≥1.
∴a的取值范围为[1,+∞).
(3)设AF=a,BF=b,由抛物线定义,2MN=a+b.
由余弦定理,|AB|2=a2+b2-2abcos120°=(a+b)2-ab,
再由a+b≥2$\sqrt{ab}$,得到ab≤$\frac{(a+b)^{2}}{4}$,
即有|AB|≥$\frac{\sqrt{3}}{2}$(a+b).即$\frac{|MN|}{|AB|}$≤$\frac{\sqrt{3}}{3}$.
所以$\frac{|MN|}{|AB|}$的最大值为$\frac{\sqrt{3}}{3}$.
点评 本题考查轨迹方程的求法,向量垂直的条件,余弦定理和基本不等式的运用,考查了学生综合分析问题和解决问题的能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
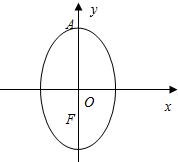 已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.
已知动圆Q过定点F(0,-1),且与直线l:y=1相切,椭圆N的对称轴为坐标轴,O点为坐标原点,F是其一个焦点,又点A(0,2)在椭圆N上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{99}{100}$)2 | B. | 0.01 | ||
| C. | C${\;}_{6}^{1}$$\frac{1}{100}$•(1-$\frac{1}{100}$)5 | D. | C${\;}_{6}^{2}$($\frac{1}{100}$)2•(1-$\frac{1}{100}$)4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com