
分析 (1)利用绝对值的几何意义,可求x的取值范围;
(2)在(1)的条件下,利用柯西不等式求g(x)=3$\sqrt{x+4}$+4$\sqrt{|x-6|}$的最大值.
解答 解:(1)f(x)<0,即|x-2|<3,所以-1<x<5;
(2)在(1)的条件下,g(x)=3$\sqrt{x+4}$+4$\sqrt{6-x}$,
∴(3$\sqrt{x+4}$+4$\sqrt{6-x}$)2≤(32+42)(x+4+6-x)=250,
∴g(x)=3$\sqrt{x+4}$+4$\sqrt{|x-6|}$的最大值为5$\sqrt{10}$.
点评 本题考查绝对值的几何意义,柯西不等式,考查学生的计算能力,比较基础.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心,以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{1}{2}$,以原点为圆心,以椭圆的短半轴为半径的圆与直线x-y+$\sqrt{6}$=0相切.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
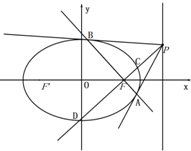
 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com