
 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.分析 (Ⅰ)由椭圆的性质离心率和焦点顶点等求得椭圆方程.
(Ⅱ)当圆M和圆N是两个相外切的等圆时,一定有A,M,N在一条直线上,且AM=AN.则M、N关于点A对称,设M(x1,y1),则N(-x1,8-y1),点M在线段AD的垂直平分线y-$\frac{5}{2}$=-$\frac{5}{4}$(x+$\frac{15}{8}$)上,可求得x1=-$\frac{251}{40}$,继而求得坐标.
解答 (Ⅰ)解:设左焦点F的坐标为(-c,0),其中c=$\sqrt{{a^2}-{b^2}}$,
∵e=$\frac{c}{a}=\frac{3}{5}$,∴a=$\frac{5}{3}$c,b=$\frac{4}{3}$c…(1分)
∴A(0,$\frac{4}{3}$c),B(-$\frac{5}{3}$c,0),C(0,-$\frac{4}{3}$c),…(2分)
∴AB:$-\frac{3x}{5c}+\frac{3y}{4c}=1$,CF:$-\frac{x}{c}-\frac{3y}{4c}=1$,…(3分)
联立解得D点的坐标为(-$\frac{5}{4}$c,$\frac{1}{3}$c)…(4分)
∵△ADC的面积为15,∴$\frac{1}{2}$|xD|•|AC|=15,即$\frac{1}{2}$•$\frac{5}{4}$c•2•$\frac{4}{3}$c=15,
解得c=3,∴a=5,b=4,∴椭圆C的方程为$\frac{x^2}{25}+\frac{y^2}{16}=1$…(6分)
(Ⅱ)由(Ⅰ)知,A点的坐标为(0,4),D点的坐标为(-$\frac{15}{4}$,1)…(7分)
假设存在这样的两个圆M与圆N,其中AD是圆M的弦,AC是圆N的弦,
则点M在线段AD的垂直平分线上,点N在线段AC的垂直平分线y=0上…(8分)
当圆M和圆N是两个相外切的等圆时,一定有A,M,N在一条直线上,且AM=AN.
∴M、N关于点A对称,设M(x1,y1),则N(-x1,8-y1),…(9分)
根据点N在直线y=0上,∴y1=8.∴M(x1,8),N(-x1,0),
而点M在线段AD的垂直平分线y-$\frac{5}{2}$=-$\frac{5}{4}$(x+$\frac{15}{8}$)上,可求得x1=-$\frac{251}{40}$…(10分)
故存在这样的两个圆,且这两个圆的圆心坐标分别为
M(-$\frac{251}{40}$,8),N($\frac{251}{40}$,0)…(12分)
点评 本题主要考查利用椭圆的性质求得椭圆方程和直线与圆锥曲线的综合问题,属于中档题型,在高考中经常考到.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 5ln3 | C. | -5ln3 | D. | $\frac{1}{5ln3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
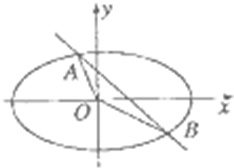 如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.
如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com