
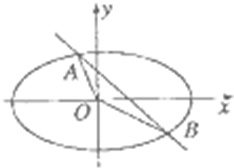
 如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.
如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.分析 (Ⅰ)∵e=$\frac{\sqrt{3}}{3}$,2c=2,则$\frac{c}{a}=\frac{\sqrt{3}}{3}$,∴$a=\sqrt{3}$,则b=$\sqrt{{a}^{2}-{c}^{2}}=\sqrt{2}$.解得椭圆方程.
(Ⅱ)设A(x1,y1),B(x2,y2),由$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{y=-x+1}\end{array}\right.$,消去y得:(a2+b2)x2-2a2x+a2(1-b2)=0,由∵$\overrightarrow{OA}⊥\overrightarrow{OB}$,∴$\overrightarrow{OA}•\overrightarrow{OB}=0$,即x1x2+y1y2=0,代入列式求解.
解答 解:(Ⅰ)∵e=$\frac{\sqrt{3}}{3}$,2c=2,则$\frac{c}{a}=\frac{\sqrt{3}}{3}$,∴$a=\sqrt{3}$,则b=$\sqrt{{a}^{2}-{c}^{2}}=\sqrt{2}$.
∴椭圆得方程为$\frac{{x}^{2}}{3}+\frac{{y}^{2}}{2}=1$
将y=-x+1代入消去y得:5x2-6x-3=0
设A(x1,y1),B(x2,y2)
∴$|AB|=\sqrt{1+(-1)^{2}}×\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{2}×\sqrt{(\frac{6}{5})^{2}+\frac{12}{5}}=\frac{8\sqrt{3}}{5}$,
又原点到直线l的距离d=$\frac{\sqrt{2}}{2}$,故${S}_{△AOB}=\frac{2\sqrt{6}}{5}$
(Ⅱ)设A(x1,y1),B(x2,y2)
∵$\overrightarrow{OA}⊥\overrightarrow{OB}$,∴$\overrightarrow{OA}•\overrightarrow{OB}=0$,即x1x2+y1y2=0
由$\left\{\begin{array}{l}{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\\{y=-x+1}\end{array}\right.$,消去y得:(a2+b2)x2-2a2x+a2(1-b2)=0
由△=(-2a2)2-4a2(a2+b2)(1-b2)>0,整理得a2+b2>1
又x1+x2=$\frac{2{a}^{2}}{{a}^{2}+{b}^{2}},{x}_{1}{x}_{2}=\frac{{a}^{2}(1-{b}^{2})}{{a}^{2}+{b}^{2}}$
y1y2=(-x1+1)(-x2+1)=x1x2-(x1+x2)+1
由x1x2+y1y2=0,得:2x1x2-(x1+x2)+1=0
∴$\frac{2{a}^{2}(1-{b}^{2})}{{a}^{2}+{b}^{2}}-\frac{2{a}^{2}}{{a}^{2}+{b}^{2}}+1=0$整理得:a2+b2-2a2b2=0,
∵b2=a2-c2=a2-a2e2代入上式得:2${a}^{2}=1+\frac{1}{1-{e}^{2}}$∴${e}^{2}=1-\frac{1}{2{a}^{2}-1}∴2a∈[2\sqrt{2},2\sqrt{3}]$
∴${e}^{2}∈[\frac{2}{3},\frac{4}{5}]$,符合条件a2+b2>1
由此得:$e∈[\frac{\sqrt{6}}{3},\frac{2\sqrt{5}}{5}]$
点评 本题主要考查了椭圆方程的求法和直线与圆锥曲线的综合问题属于中档题型,高考经常涉及.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.
如图,椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率e=$\frac{3}{5}$,左焦点为F,A,B,C为其三个顶点,直线CF与AB交于点D,若△ADC的面积为15.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,\frac{1}{2}]$ | B. | $[{\frac{1}{5},\frac{1}{2}}]$ | C. | $[{\frac{1}{5},+∞})$ | D. | $(-∞,\frac{1}{5}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | EF∥GH | B. | EH∥FG | C. | EH∥平面BCD | D. | FG∥平面ABD |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com