
分析 (1)根据已知三个等式,找出一般性规律,写出即可;
(2)由(1)中等式左边利用两角和与差的余弦函数公式化简,再利用同角三角函数间基本关系变形得到结果与右边相等,得证.
解答 解:(1)根据题意得:sin2x+cos2(x+30°)+sinxcos(x+30°)=$\frac{3}{4}$;
(2)已知等式左边=sin2x+($\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx)2+sinx($\frac{\sqrt{3}}{2}$cosx-$\frac{1}{2}$sinx)
=sin2x+$\frac{3}{4}$cos2x+$\frac{1}{4}$sin2x-$\frac{\sqrt{3}}{2}$sinxcosx+$\frac{\sqrt{3}}{2}$sinxcosx-$\frac{1}{2}$sin2x
=$\frac{3}{4}$cos2x+$\frac{3}{4}$sin2x=$\frac{3}{4}$=右边,
则sin2x+cos2(x+30°)+sinxcos(x+30°)=$\frac{3}{4}$.
点评 此题考查了三角函数的化简求值,熟练掌握运算法则是解本题的关键.


科目:高中数学 来源: 题型:解答题
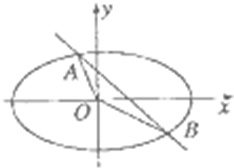 如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.
如图,直线l:y=-x+1与椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)相交于A、B两点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,某广场为一半径为80米的半圆形区域,现准备在其一扇形区域OAB内建两个圆形花坛,该扇形的圆心角为变量2θ(0<2θ<π),其中半径较大的花坛⊙P内切于该扇形,半径较小的花坛⊙Q与⊙P外切,且与OA、OB相切.
如图,某广场为一半径为80米的半圆形区域,现准备在其一扇形区域OAB内建两个圆形花坛,该扇形的圆心角为变量2θ(0<2θ<π),其中半径较大的花坛⊙P内切于该扇形,半径较小的花坛⊙Q与⊙P外切,且与OA、OB相切.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com