
【题目】已知函数![]() 为奇函数,且
为奇函数,且![]() ,其中
,其中![]() ,
,![]() .
.
(1)求![]() ,
,![]() 的值.
的值.
(2)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题(1)先根据奇函数性质得y2=cos(2x+θ)为奇函数,解得θ=![]() ,再根据
,再根据![]() 解得a(2)根据条件化简得sinα=
解得a(2)根据条件化简得sinα=![]() ,根据同角三角函数关系得cosα,最后根据两角和正弦公式求sin
,根据同角三角函数关系得cosα,最后根据两角和正弦公式求sin![]() 的值
的值
试题解析:(1)因为f(x)=(a+2cos2x)cos(2x+θ)是奇函数,而y1=a+2cos2x为偶函数,所以y2=cos(2x+θ)为奇函数,由θ∈(0,π),得θ=![]() ,所以f(x)=-sin 2x·(a+2cos2x),
,所以f(x)=-sin 2x·(a+2cos2x),
由f![]() =0得-(a+1)=0,即a=-1.
=0得-(a+1)=0,即a=-1.
(2)由(1)得f(x)=-![]() sin 4x,因为f
sin 4x,因为f![]() =-
=-![]() sin α=-
sin α=-![]() ,
,
即sin α=![]() ,又α∈
,又α∈![]() ,从而cos α=-
,从而cos α=-![]() ,
,
所以sin![]() =sin αcos
=sin αcos![]() +cos αsin
+cos αsin![]() =
=![]() ×
×![]() +
+![]() ×
×![]() =
=![]() .
.


科目:高中数学 来源: 题型:
【题目】已知A(-2,0),B(2,0)为椭圆C的左、右顶点,F为其右焦点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为![]() 。
。
(Ⅰ)求椭圆C的方程;
(Ⅱ)直线AP与椭圆在点B处的切线交于点D,当点P在椭圆上运动时,求证:以BD为直径的圆与直线PF恒相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从你所在班级任意选出6名同学,调查他们的出生月份,假设出生在一月,二月……十二月是等可能的.设事件![]() “至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件
“至少有两人出生月份相同”,设计一种试验方法,模拟20次,估计事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】盒子中仅有4个白球和5个黑球,从中任意取出一个球.
(1)“取出的球是黄球”是什么事件?它的概率是多少?
(2)“取出的球是白球”是什么事件?它的概率是多少?
(3)“取出的球是白球或黑球”是什么事件?它的概率是多少?
(4)设计一个用计算器或计算机模拟上面取球的试验,并模拟100次,估计“取出的球是白球”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】写出下列命题的否定,并判断所得命题的真假:
(1)![]() ;
;
(2)有的三角形是等边三角形;
(3)有一个偶数是素数
(4)任意两个等边三角形都相似;
(5)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆C过定点F(2,0),且与直线x=-2相切,圆心C的轨迹为E,
(1)求圆心C的轨迹E的方程;
(2)若直线l交E与P,Q两点,且线段PQ的中心点坐标(1,1),求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着经济模式的改变,微商和电商已成为当今城乡一种新型的购销平台.已知经销某种商品的电商在任何一个销售季度内,没售出1吨该商品可获利润0.5万元,未售出的商品,每1吨亏损0.3万元.根据往年的销售经验,得到一个销售季度内市场需求量的频率分布直方图如图所示.已知电商为下一个销售季度筹备了130吨该商品,现以![]() (单位:吨,
(单位:吨,![]() )表示下一个销售季度的市场需求量,
)表示下一个销售季度的市场需求量,![]() (单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
(单位:万元)表示该电商下一个销售季度内经销该商品获得的利润.
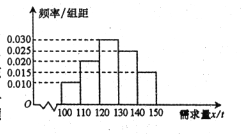
(Ⅰ)视![]() 分布在各区间内的频率为相应的概率,求
分布在各区间内的频率为相应的概率,求![]() ;
;
(Ⅱ)将![]() 表示为
表示为![]() 的函数,求出该函数表达式;
的函数,求出该函数表达式;
(Ⅲ)在频率分布直方图的市场需求量分组中,以各组的区间中点值(组中值)代表该组的各个值,并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率(例如![]() ,则取
,则取![]() 的概率等于市场需求量落入
的概率等于市场需求量落入![]() 的频率),求
的频率),求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com