
设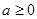 ,若
,若 的最大值为0,最小值为-4,试求
的最大值为0,最小值为-4,试求 与
与 的值,并求
的值,并求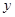 的最大、最小值及相应的
的最大、最小值及相应的 值.
值.
详见解析.
解析试题分析:利用 ,化简函数可得y=-
,化简函数可得y=-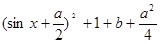 ,由于-1≤sinx≤1,a≥0,就0≤a≤2和a>2分类讨论,求出两类情况对应的a与b的值,在求出相应的x.
,由于-1≤sinx≤1,a≥0,就0≤a≤2和a>2分类讨论,求出两类情况对应的a与b的值,在求出相应的x.
原函数变形为y=-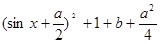 2
2
∵-1≤sinx≤1,a≥0
∴若0≤a≤2,当sinx=- 时ymax=1+b+
时ymax=1+b+ =0 ①
=0 ①
当sinx=1时,ymin=-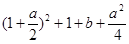 =-a+b=-4 ②
=-a+b=-4 ②
联立①②式解得a=2,b=-2 7
y取得最大、小值时的x值分别为:
x=2kπ-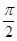 (k∈Z),x=2kπ+
(k∈Z),x=2kπ+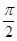 (k∈Z)
(k∈Z)
若a>2时, ∈(1,+∞)
∈(1,+∞)
∴ymax=-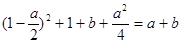 =0 ③
=0 ③
ymin=-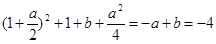 ④
④
由③④得a=2时,而 =1 (1,+∞)舍去 11
=1 (1,+∞)舍去 11
故只有一组解a=2,b=-2 ..12
考点:1.二次函数的最值;2.正弦函数.


科目:高中数学 来源: 题型:解答题
(2013·佛山模拟)在平面直角坐标系xOy中,以Ox为始边,角α的终边与单位圆O的交点B在第一象限,已知A(-1,3).
(1)若OA⊥OB,求tan α的值;
(2)若B点横坐标为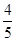 ,求S△AOB.
,求S△AOB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com