
分析 利用切线与圆心的连线垂直,可得SPACB=2SACP.,要求四边形PACB的最小面积,即直线上的动点到圆心的距离最短,利用二次函数的配方求解最小值,得到三角形的边长最小值,可以求四边形PACB的最小面积.
解答 解:根据题意:圆C:(x-1)2+(y-1)2=4,圆心为(1,1),半径r=2,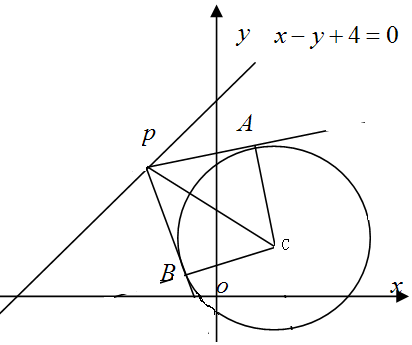
∵点P在直线x-y+4=0上,设P(t,t+4),切线与圆心的连线垂直,
直线上的动点到圆心的距离d2=(t-1)2+(t+4-1)2,
化简:d2=2(t2+2t+5)
=2(t+1)2+8,
∴${d}_{min}=2\sqrt{2}$,
那么:$PA=\sqrt{{d}^{2}{-r}^{2}}$,
则|PA|min=2,
三角形PAC的最小面积为:${S}_{PAC}=\frac{1}{2}PA•r$=2,
可得:SPACB=2SACP=4,
所以:四边形PACB的最小面积SPABC=4,
故答案为:4.
点评 本题考查了圆的切线问题,切线与圆心的连线垂直,能构造直角三角形,把四边形PACB的最小面积,直线上的动点到圆心的距离最短是解题的关键.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | A=B | B. | A=C | C. | B=C | D. | A=B=C |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {y|y≠2} | B. | {y|y≠3} | C. | (-∞,2) | D. | $\{y|y≠\frac{5}{3}\}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com