
| A. | -4 | B. | 3-2$\sqrt{10}$ | C. | 3-4$\sqrt{2}$ | D. | -2 |
分析 画出函数的图象,判断a,b的范围,利用直线与圆的位置关系,通过相切求解最小值.
解答 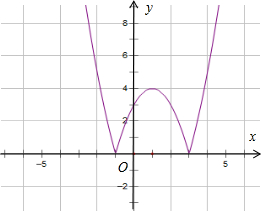 解:由函数f(x)的图象:
解:由函数f(x)的图象:
可知,a<-1,-1<b<1,
且a2-2a-3=-b2+2b+3,即点P(a,b)满足不等式组$\left\{{\begin{array}{l}{a<-1}\\{-1<b<1}\\{{{(a-1)}^2}+{{(b-1)}^2}=8}\end{array}}\right.$,
此区域为以$A(-1,-1),B(-2\sqrt{2}+1,1)$为端点
且不含端点的圆弧,
直线u=2a+b与圆弧相切于点C,
则直线u=2a+b过点C时,
u有最小值,2$\sqrt{2}$=$\frac{|2+1-u|}{\sqrt{{2}^{2}+{1}^{2}}}$,(u<0),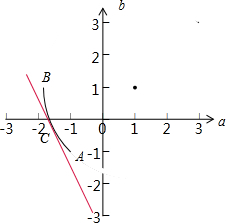
解得u=3-2$\sqrt{10}$.
最小值为:$3-2\sqrt{10}$.
故选:B.
点评 本题考查函数与方程的综合应用,考查函数的图象,直线与圆的位置关系,考查分析问题解决问题的能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{2}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
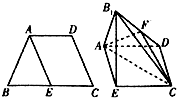 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿AE翻折成△B1AE,使面B1AE⊥面AECD,F为B1D的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com