
 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 条件语句中必须有if、else和end | |
| B. | 条件语句中可以没有end | |
| C. | 条件语句中可以没有else,但必须有end | |
| D. | 条件语句中可以没有else及没end |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲 | 82 | 81 | 79 | 78 | 95 | 88 | 93 | 84 |
| 乙 | 92 | 95 | 80 | 75 | 83 | 80 | 90 | 85 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $36+16\sqrt{2}$,32 | B. | $4\sqrt{2}+2$,$4\sqrt{2}$ | C. | $36+16\sqrt{2}$,$4\sqrt{2}$ | D. | $36+16\sqrt{2}$,36 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$分米 | B. | 1分米 | C. | 2分米 | D. | 4分米 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
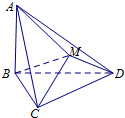 如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,
如图,在多面体ABCDM中,△BCD是等边三角形,△CMD是等腰直角三角形,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若β=α+k•360°(k∈Z),则α与β终边相同 | B. | 第二象限角一定是钝角 | ||
| C. | 终边在y轴正半轴上的角是直角 | D. | 第四象限角一定是负角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com