
| A. | $\frac{\sqrt{6}+2}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\sqrt{6}$+2 | D. | $\sqrt{6}$+$\sqrt{2}$ |
分析 不等式a(x+y)≥x+$\sqrt{\frac{1}{2}xy}$分离参数,再利用换元法,构造函数,利用导数法确定函数的最大值,从而可求实数a的最小值
解答 解:∵x>0,y>0,
∴不等式a(x+y)≥x+$\sqrt{\frac{1}{2}xy}$等价为a≥$\frac{x+\sqrt{\frac{1}{2}xy}}{x+y}$=$\frac{1+\sqrt{\frac{1}{2}•\frac{y}{x}}}{1+\frac{y}{x}}$,
令$t=\sqrt{\frac{y}{x}}(t>0)$,∴a≥$\frac{1+\frac{\sqrt{2}}{2}t}{1+{t}^{2}}$,
令u=$\frac{1+\frac{\sqrt{2}}{2}t}{1+{t}^{2}}$,∴u′=$\frac{-\frac{\sqrt{2}}{2}{t}^{2}-2t+\frac{\sqrt{2}}{2}}{(1+t{{\;}^{2})}^{2}}$
令u′=0,∴t=-$\sqrt{2}$$+\sqrt{3}$(负值舍去)
∴函数在(0,$\sqrt{3}-\sqrt{2}$)上单调增,在($\sqrt{3}-\sqrt{2}$,+∞)上单调减
∴t=$\sqrt{3}-\sqrt{2}$时,函数u=$\frac{1+\frac{\sqrt{2}}{2}t}{1+{t}^{2}}$取得最大值为$\frac{\sqrt{6}+2}{4}$
∴a≥$\frac{\sqrt{6}+2}{4}$
∴实数a的最小值为$\frac{\sqrt{6}+2}{4}$
故选:A
点评 本题考查恒成立问题,利用参数分离法转化为求函数的最值问题,构造函数求函数的导数,利用导数研究函数的单调性是解决本题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 种下一粒杨树种子,求其能长成大树的概率 | |
| B. | 掷一颗质地不均匀的骰子,求出现1点的概率 | |
| C. | 在区间[1,4]上任取一数,求这个数大于1.5的概率 | |
| D. | 同时掷两枚质地均匀的骰子,求向上的点数之和是5的概率 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\underbrace{33…3}_{n个}$ | B. | $\underbrace{33…3}_{n+1个}$ | C. | $\underbrace{33…3}_{2n个}$ | D. | $\underbrace{33…3}_{2n-1个}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
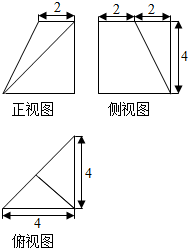
| A. | $\frac{16}{3}$ | B. | $\frac{80}{3}$ | C. | $\frac{40}{3}$ | D. | 40 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,网格纸上小方格的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小方格的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的表面积为( )| A. | 14+6$\sqrt{5}$ | B. | 28+6$\sqrt{5}$ | C. | 28+12$\sqrt{5}$ | D. | 36+12$\sqrt{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com