
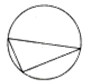
 如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字)
如图,圆被其内接三角形分为4块,现有5种颜色准备用来涂这4块,要求每块涂一种颜色,且相邻两块的颜色不同,则不同的涂色方法有320种.(填数字) 科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|$\frac{1}{3}$<x<$\frac{1}{2}$} | B. | {x|x>$\frac{1}{2}$} | C. | {x|x<$\frac{1}{3}$} | D. | {x|x<$\frac{1}{3}$或x>$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | K2在任何相互独立问题中都可以用来检验有关还是无关 | |
| B. | K2的值越大,两个事件的相关性越大 | |
| C. | K2是用来判断两个分类变量是否有关系的随机变量,只对于两个分类变量适合 | |
| D. | K2的观测值的计算公式为K2=$\frac{n(ad-bc)}{(a+b)(c+d)(a+c)(b+d)}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com