
分析 (Ⅰ)是$f′(x)=\frac{1}{x}+1-e(x+1){e}^{x}=\frac{(x+1)(1-ex•{e}^{x})}{x}$,令μ(x)=1-ex•ex,则μ′(x)=-e(x+1)ex<0(x>0),可得f(x)存在唯一零点x0∈(0,$\frac{1}{e}$),即f(x)max=f(x0)=lnx0+x0-4-ex0e${\;}^{{x}_{0}}$,又$μ({x}_{0})=1-e{x}_{0}{e}^{{x}_{0}}=0$,e${\;}^{{x}_{0}}$=$\frac{1}{e{x}_{0}}$,x0=ln$\frac{1}{e{x}_{0}}$=-1-lnx0,即可得$f(x)_{max}=ln{x}_{0}+(-1-ln{x}_{0})-4-{e}^{{x}_{0}}•\frac{1}{e{x}_{0}}$=-5-1=-6
(Ⅱ)|p(x)|>q(x)?a<|$\frac{lnx+x-4}{x{e}^{x}}$,令h(x)=<$\frac{lnx+x-4}{x{e}^{x}}$,则h$′(x)=\frac{(x+1)(lnx+x-5)}{{x}^{2}{e}^{x}}$,令φ(x)=lnx+x-5,可得存在t∈(3,4),使得φ(t)=0,又|h(1)|=$\frac{3}{e}$,|h(2)|=$\frac{2-ln2}{2{e}^{2}}$>|h(3)|=$\frac{ln3-1}{3{e}^{3}}$,|h(4)|=$\frac{2ln2}{4{e}^{4}}$,即可得a的取值范围应为$\frac{ln3-1}{3{e}^{3}}≤a<\frac{2-ln2}{2{e}^{2}}$
解答 (Ⅰ)证明:由题知f(x)=lnx+x-4-ex•ex,
于是$f′(x)=\frac{1}{x}+1-e(x+1){e}^{x}=\frac{(x+1)(1-ex•{e}^{x})}{x}$,
令μ(x)=1-ex•ex,则μ′(x)=-e(x+1)ex<0(x>0),
∴μ(x)在(0,+∞)上单调递减.
又μ(0)=1>0,$μ(\frac{1}{e})$=1-${e}^{\frac{1}{e}}$<0,
所以存在x0∈(0,$\frac{1}{e}$),使得μ(x0)=0,
综上f(x)存在唯一零点x0∈(0,$\frac{1}{e}$). …(3分)
当x∈(0,x0),μ(x)>0,于是f′(x)>0,f(x)在(0,x0)单调递增;
当x∈(x0,+∞),μ(x)<0,于是f′(x)<0,f(x)在(x0,+∞)单调递减.
故f(x)max=f(x0)=lnx0+x0-4-ex0e${\;}^{{x}_{0}}$,
又$μ({x}_{0})=1-e{x}_{0}{e}^{{x}_{0}}=0$,e${\;}^{{x}_{0}}$=$\frac{1}{e{x}_{0}}$,x0=ln$\frac{1}{e{x}_{0}}$=-1-lnx0,
故$f(x)_{max}=ln{x}_{0}+(-1-ln{x}_{0})-4-{e}^{{x}_{0}}•\frac{1}{e{x}_{0}}$=-5-1=-6.…(6分)
(Ⅱ) 解:|p(x)|>q(x)等价于|lnx+x-4|>axex.
?a<|$\frac{lnx+x-4}{x{e}^{x}}$|,…(7分)
令h(x)=<$\frac{lnx+x-4}{x{e}^{x}}$,则h$′(x)=\frac{(x+1)(lnx+x-5)}{{x}^{2}{e}^{x}}$,
令φ(x)=lnx+x-5,则φ$′(x)=\frac{1}{x}+1$>0,即φ(x)在(0,+∞)上单调递增.
又φ(3)=ln3-2<0,φ(4)=ln4-1>0,
∴存在t∈(3,4),使得φ(t)=0.…(9分)
∴当x∈(0,t),φ(x)<0⇒h′(x)>0⇒h(x)在(0,t)单调递增;
当x∈(t,+∞),φ(x)>0⇒h′(x)<0⇒h(x)在(t,+∞)单调递减.
∵h(1)=-$\frac{3}{e}$<0,h(2)=$\frac{ln2-2}{2{e}^{2}}<0$,h(3)=$\frac{ln3-1}{3{e}^{3}}>0$,
且当x>3时,h(x)>0,
又|h(1)|=$\frac{3}{e}$,|h(2)|=$\frac{2-ln2}{2{e}^{2}}$>|h(3)|=$\frac{ln3-1}{3{e}^{3}}$,|h(4)|=$\frac{2ln2}{4{e}^{4}}$,
故要使不等式式|p(x)|>q(x)解集中有且只有两个整数,a的取值范围应为:
$\frac{ln3-1}{3{e}^{3}}≤a<\frac{2-ln2}{2{e}^{2}}$.…(12分)
点评 考查了利用导数求零点、函数最值,考查了转化思想、计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
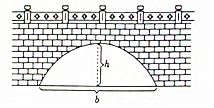 一拱桥的形状为抛物线,该抛物线拱的高为h,宽为b,此抛物线拱的面积为S,若b=3h,则S等于( )
一拱桥的形状为抛物线,该抛物线拱的高为h,宽为b,此抛物线拱的面积为S,若b=3h,则S等于( )| A. | h2 | B. | $\frac{3}{2}$h2 | C. | $\sqrt{3}$h2 | D. | 2h2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com