Question

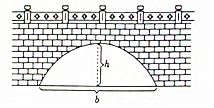
12．一拱桥的形状为抛物线，该抛物线拱的高为h，宽为b，此抛物线拱的面积为S，若b=3h，则S等于（　　）

• A． h²
• B． $\frac{3}{2}$h²
• C． $\sqrt{3}$h²
• D． 2h²

Answer 1

分析 建立平面直角坐标系，设抛物线方程，将点代入抛物线方程，即可求得抛物线方程，根据定积分的几何意义，即可求得S．

解答 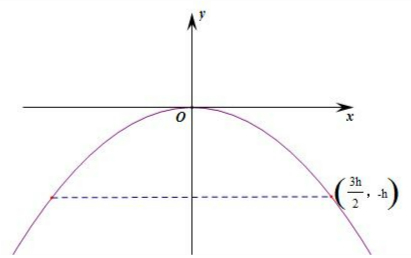解：以抛物线的最高点为坐标原点，以抛物线的拱的对称轴为y轴，建立平面直角坐标系，
设抛物线方程y=ax²，a＜0，
由抛物线经过点（$\frac{3h}{2}$，-h），代入抛物线方程：-h=a（$\frac{3h}{2}$）²，
解得：a=-$\frac{4}{9h}$，
S=h×3h-（-2${∫}_{0}^{\frac{3h}{2}}$ax²dx），=3h²-2×$\frac{4}{9h}$×$\frac{1}{3}$x³${丨}_{0}^{\frac{3h}{2}}$=2h²，
故选D．

点评 本题考查抛物线的方程，定积分的几何意义，利用定积分求曲边梯形的面积，考查数形结合思想，属于中档题．