考点:函数的最值及其几何意义
专题:综合题,函数的性质及应用
分析:确定函数的定义域,利用换元法,转化为二次函数求最值,即可得出结论.
解答:
解:由题意得函数f(x)的定义域为[-1,1].
由t=
+
平方得t
2=2+2
.
由x∈[-1,1]得,t
2∈[2,4],
所以t的取值范围是[
,2].
又
=
t
2-1,∴h(t)=at
2+t-a,定义域为[
,2].
由题意知g(a)即为函数h(t)=
at
2+t-a,t∈[
,2]的最大值.
注意到直线t=-
是抛物线h(t)=
at
2+t-a的对称轴,分以下几种情况讨论:
①当a>0时,函数y=h(t),t∈[
,2]的图象是开口向上的抛物线的一段,
由t=-
<0知y=h(t)在[
,2]上单调递增,∴g(a)=h(2)=a+2.
②当a=0时,h(t)=t,t∈[
,2],∴g(a)=h(2)=2.
③当a<0时,函数y=h(t),t∈[
,2]的图象是开口向下的抛物线的一段,t=-
>0.
若t=-
∈(0,
),即a<-
时,则g(a)=h(
)=
;
若t=-
∈[
,2],即-
≤a≤-
时,则g(a)=h(-
)=-a-
;
若t=-
∈(2,+∞),即-
<a<0时,则g(a)=h(2)=a+2.
综上所述,g(a)=
.
点评:本题考查函数的最值,考查分类讨论的数学思想,考查学生分析解决问题的能力,正确转化是关键.



 阅读快车系列答案
阅读快车系列答案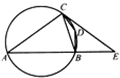 如图,四边形么BDC内接于圆,BD=CD,过C点的圆的切线与AB的延长线交于E点.
如图,四边形么BDC内接于圆,BD=CD,过C点的圆的切线与AB的延长线交于E点.