
分析 (1)求出函数的导数,求出极值点,g(x)存在两个极值点x1,x2(x1<x2),推出$\left\{\begin{array}{l}△=16-32m>0\\ \frac{m}{8}>0\end{array}\right.$,求出m的范围,化简x1-x2,通过$x∈({-\frac{1}{2},-\frac{1}{4}})$时,f'(x)<0,当$x∈({-\frac{1}{4},0})$时,f'(x)>0,求解f(x1-x2)的最小值.
(2)通过g(x1)≥ax2得$a≤\frac{{g({x_1})}}{x_2}$,化简$\frac{{g({x_1})}}{x_2}=\frac{{4{x_1}^2-4{x_1}+mln(2{x_1})}}{{\frac{1}{2}-{x_1}}}$=$2[{(1-2{x_1})-\frac{1}{{1-2{x_1}}}+2(2{x_1})ln(2{x_1})}]$,构造ϕ(x)=$2[{(1-x)-\frac{1}{1-x}+2xlnx}]$($0<x<\frac{1}{2}$),求出导函数,利用函数的单调性求解最值即可.
解答 (本小题满分12分)
解:(Ⅰ)$g'(x)=8x-4+\frac{m}{x}=\frac{{8{x^2}-4x+m}}{x}(x>0)$,
令g'(x)=0得8x2-4x+m=0①,
因为g(x)存在两个极值点x1,x2(x1<x2),
所以方程①在(0,+∞)上有两个不等实根x1,x2,
所以$\left\{\begin{array}{l}△=16-32m>0\\ \frac{m}{8}>0\end{array}\right.$解得$0<m<\frac{1}{2}$,
且${x_1}+{x_2}=\frac{1}{2},0<{x_1}<\frac{1}{4}$,…(3分)
所以${x_1}-{x_2}={x_1}-(\frac{1}{2}-{x_1})=2{x_1}-\frac{1}{2}∈({-\frac{1}{2},0})$$f'(x)=(x+\frac{1}{4}){e^x}$,
当$x∈({-\frac{1}{2},-\frac{1}{4}})$时,f'(x)<0,当$x∈({-\frac{1}{4},0})$时,f'(x)>0,
所以f(x1-x2)的最小值为$f(-\frac{1}{4})=-{e^{-\frac{1}{4}}}$…(5分)
(Ⅱ)由(Ⅰ)可知,$0<m<\frac{1}{2},{x_1}+{x_2}=\frac{1}{2},{x_1}{x_2}=\frac{m}{8}(0<{x_1}<\frac{1}{4},\frac{1}{4}<{x_2}<\frac{1}{2})$,
由g(x1)≥ax2得$a≤\frac{{g({x_1})}}{x_2}$,…(6分)
所以$\frac{{g({x_1})}}{x_2}=\frac{{4{x_1}^2-4{x_1}+mln(2{x_1})}}{{\frac{1}{2}-{x_1}}}$
=$\frac{{4{x_1}^2-4{x_1}+8{x_1}{x_2}ln(2{x_1})}}{{\frac{1}{2}-{x_1}}}$
=$\frac{{4{x_1}^2-4{x_1}+8{x_1}(\frac{1}{2}-{x_1})ln(2{x_1})}}{{\frac{1}{2}-{x_1}}}$
=$\frac{{{{(2{x_1}-1)}^2}-1+2(2{x_1})(1-2{x_1})ln(2{x_1})}}{{\frac{1}{2}(1-2{x_1})}}$
=$2[{(1-2{x_1})-\frac{1}{{1-2{x_1}}}+2(2{x_1})ln(2{x_1})}]$…(9分)
令ϕ(x)=$2[{(1-x)-\frac{1}{1-x}+2xlnx}]$($0<x<\frac{1}{2}$),
则ϕ'(x)=$2[{1-\frac{1}{{{{(1-x)}^2}}}+2lnx}]$
因为$0<x<\frac{1}{2}$,
所以$-1<x-1<-\frac{1}{2},\frac{1}{4}<{(x-1)^2}<1$,φ'(x)<0,即φ(x)在$({0,\frac{1}{2}})$递减,$φ(x)>φ(\frac{1}{2})=-3-2ln2$,
综上,实数a的取值范围为(-∞,-3-2ln2]…(12分)
点评 本题考查函数的导数的综合应用,函数的单调性以及函数的最值的求法,考查转化思想以及计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥α,b?α,则a⊥b | B. | 若a⊥α,a∥b,则b⊥α | ||
| C. | 若a⊥b,b⊥α,则a∥α或a?α | D. | 若a∥α,b?α,则a∥b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
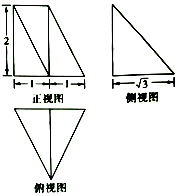 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )| A. | 3$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{4}{3}$$\sqrt{3}$ | D. | $\frac{5}{3}$$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com