
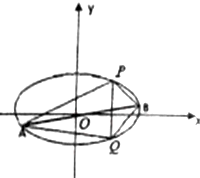
 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.分析 (I)抛物线x2=8$\sqrt{3}$y的焦点为$(0,2\sqrt{3})$.由题意可设椭圆的标准方程可得:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),则b=2$\sqrt{3}$,又$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,联立解出即可得出.
(II)①把x=2代入椭圆方程可得:|PQ|=6.设A(x1,y1),B(x2,y2).直线AB的方程为:y=$\frac{1}{2}$x+t,代入椭圆方程可得:x2+tx+t2-12=0,△>0.|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$.四边形APBQ面积S=$\frac{1}{2}×$6×|x1-x2|,利用二次函数的单调性即可得出四边形APBQ面积S取得的最大值.
②当∠APQ=∠BPQ时,直线PA,PB的斜率之和为0.设直线PA的斜率为k,则直线PB的斜率为-k.直线PA的方程为:y-3=k(x-2),与椭圆方程联立化为:(3+4k2)x2+8(3-2k)kx+4(3-2k)2-48=0,利用根与系数的关系可得x1+2,同理PB的直线方程为:y-3=-k(x-2),可得x2+2.利用斜率计算公式可得kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$.
解答 解:(I)抛物线x2=8$\sqrt{3}$y的焦点为$(0,2\sqrt{3})$.
由题意可设椭圆的标准方程可得:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),
则b=2$\sqrt{3}$,又$\frac{c}{a}$=$\frac{1}{2}$,a2=b2+c2,
解得a=4,c=2.
∴椭圆C标准方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}$=1.
(II)①把x=2代入椭圆方程可得:$\frac{4}{16}$+$\frac{{y}^{2}}{12}$=1,解得y=±3.∴|PQ|=6.
设A(x1,y1),B(x2,y2).直线AB的方程为:y=$\frac{1}{2}$x+t,代入椭圆方程可得:x2+tx+t2-12=0,
由△>0,可得:-4<t<4.
∴x1+x2=-t,x1x2=t2-12.
|x1-x2|=$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{48-3{t}^{2}}$.
∴四边形APBQ面积S=$\frac{1}{2}×$6×|x1-x2|=3$\sqrt{48-3{t}^{2}}$.
当t=0时,四边形APBQ面积S取得最大值12$\sqrt{3}$.
②当∠APQ=∠BPQ时,直线PA,PB的斜率之和为0.设直线PA的斜率为k,则直线PB的斜率为-k.
直线PA的方程为:y-3=k(x-2),联立$\left\{\begin{array}{l}{y-3=k(x-2)}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1}\end{array}\right.$.,化为:(3+4k2)x2+8(3-2k)kx+4(3-2k)2-48=0,
∴x1+2=$\frac{8k(2k-3)}{3+4{k}^{2}}$,
同理PB的直线方程为:y-3=-k(x-2),可得x2+2=$\frac{8k(2k+3)}{3+4{k}^{2}}$.
∴x1+x2=$\frac{16{k}^{2}-12}{3+4{k}^{2}}$,x1-x2=$\frac{-48k}{3+4{k}^{2}}$,
kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{k({x}_{1}-2)+3+k({x}_{2}-2)-3}{{x}_{1}-{x}_{2}}$=$\frac{k({x}_{1}+{x}_{2})-4k}{{x}_{1}-{x}_{2}}$=$\frac{1}{2}$.
∴直线AB的斜率为定值$\frac{1}{2}$.
点评 本题考查了抛物线与椭圆的标准方程及其性质、直线椭圆相交问题、一元二次方程的根与系数的关系、弦长公式、斜率计算公式、二次函数的单调性,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 资金 | 单位产品所需资金 | 资金供应量 | |
| 空调机 | 洗衣机 | ||
| 成本 | 30 | 20 | 440 |
| 劳动力:工资 | 7 | 10 | 156 |
| 单位利润 | 10 | 8 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 128 | B. | 81 | C. | 64 | D. | 49 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com