
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 利用正四面体的特征,作图即可得到答案
解答 解:①正四面体A-BCD的高线中心正好在底面正三角形的三线合一“三等分”上,形成直角三角形,根据“三垂线定理”,每组对棱异面垂直;正确
②底面是正三角形,连接每组对棱的中点,刚好三线交于一点;正确
③只有到高线投影落在CD上时,才存在一个点E,使得∠AEB=$\frac{π}{2}$;而正四面体A-BCD的高线中心正好在底面正三角形的三线合一上,不可能在CD,不成立
④正四面体的外接球的半径是其棱长的$\frac{{\sqrt{6}}}{4}$倍.正四面体球心在高线上,利用球心到各顶点的距离相等构造勾股定理即可找到关系.正确
所以:①②④正确
故答案为:C
点评 本题考查了正四面体特征和外接球的证明,由于正四面体本身的对称性可知,内切球和外接球的两个球心是重合的.难度不大,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3×4=12种 | B. | 4×3×2=24种 | C. | 43=64种 | D. | 34=81种 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,AB为圆O的直径,过点B作圆O的切线,任取圆O上异于A,B的一点E,连接AE并延长交BC于点C,过点E作圆O的切线,交边BC于一点D.
如图,AB为圆O的直径,过点B作圆O的切线,任取圆O上异于A,B的一点E,连接AE并延长交BC于点C,过点E作圆O的切线,交边BC于一点D.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
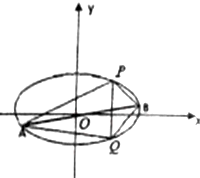 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l∥α,m∥α,则l∥m | B. | l⊥α,m⊥α,则l∥m | C. | l⊥n,m⊥n,则l∥m | D. | l?α,m∥α,则l∥m |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com