
分析 根据向量长度相等建立方程关系求出k的值,结合向量夹角公式进行求解即可.
解答 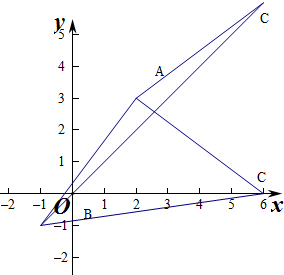 解:∵$\overrightarrow{AB}$=(-3,-4),$\overrightarrow{AC}$=(4,k-3),
解:∵$\overrightarrow{AB}$=(-3,-4),$\overrightarrow{AC}$=(4,k-3),
则|$\overrightarrow{AB}$|=5,|$\overrightarrow{AC}$|=$\sqrt{16+(k-3)^{2}}$,
由|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|得$\sqrt{16+(k-3)^{2}}$=5,
得(k-3)2=9,则k-3=3或k-3=-3,
即k=6或k=0,
若k=6,则C(6,6),$\overrightarrow{AC}$=(4,3),
则cos<$\overrightarrow{AB}$,$\overrightarrow{AC}$>=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{-3×4-4×3}{5×5}$=-$\frac{24}{25}$,
若k=0,则C(6,-1),$\overrightarrow{AC}$=(4,-3),
则cos<$\overrightarrow{AB}$,$\overrightarrow{AC}$>=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{-3×4-4×(-3)}{5×5}$=0,
故答案为:0或-$\frac{24}{25}$,
点评 本题主要考查向量数量积的应用,根据向量长度公式以及夹角公式是解决本题的关键.注意要对k进行分类讨论.


科目:高中数学 来源: 题型:解答题
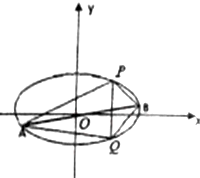 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | l∥α,m∥α,则l∥m | B. | l⊥α,m⊥α,则l∥m | C. | l⊥n,m⊥n,则l∥m | D. | l?α,m∥α,则l∥m |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列五个命题中正确的是①②
如图四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列五个命题中正确的是①②查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(a)<f(b)<f(c) | B. | f(b)<f(c)<f(a) | C. | f(b)<f(a)<f(c) | D. | f(c)<f(a)<f(b) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | [-1,2] | C. | [1,2] | D. | (1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
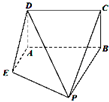 如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com