练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．如图四边形ABCD是正方形，延长CD至E，使得DE=CD．若动点P从点A出发，沿正方形的边按逆时针方向运动一周回到A点，其中$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$，下列五个命题中正确的是①②
    ①点P与点B重合时，λ+μ=1；
    ②当点P为BC的中点时，λ+μ=2；
    ③λ+μ的最大值为4； 
    ④λ+μ的最小值为-1；
    ⑤满足λ+μ=1的点P有且只有一个．

    分析 建立如图所示的直角坐标系，设正方形的边长为1，可以得到$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$的坐标表示，再根据相对应的条件加以判断即可．

    解答 解：由题意，设正方形的边长为1，建立坐标系如图，
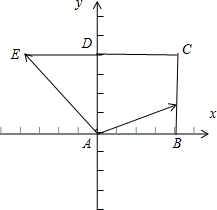    则B（1，0），E（-1，1），
    ∴$\overrightarrow{AB}$=（1，0），$\overrightarrow{AE}$=（-1，1），
    ∵$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$=（λ-μ，μ），
    ∴点P与点B重合时，$\overrightarrow{AP}$=$\overrightarrow{AB}$，
    此时λ=1，μ=0，λ+μ=1，①正确；
    ∴P是BC的中点时，$\overrightarrow{AP}$=（1，$\frac{1}{2}$）=$\frac{3}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AE}$，
    此时λ=$\frac{3}{2}$，μ=$\frac{1}{2}$，λ+μ=2，②正确；
    当P∈AB时，有0≤λ-μ≤1，μ=0，0≤λ≤1，0≤λ+μ≤1，
    当P∈BC时，有λ-μ=1，0≤μ≤1，∴λ=μ+1，∴1≤λ≤2，∴1≤λ+μ≤3，
    当P∈CD时，有0≤λ-μ≤1，μ=1，∴μ≤λ≤μ+1，即1≤λ≤2，∴2≤λ+μ≤3，
    当P∈AD时，有λ-μ=0，0≤μ≤1，∴0≤λ≤1，∴0≤λ+μ≤2，
    综上，0≤λ+μ≤3，③λ+μ的最大值为4，错误； 
    ④λ+μ的最小值为-1，错误；
    当点P为AD中点时，$\overrightarrow{AP}$=（0，$\frac{1}{2}$）=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AE}$，
    此时λ=μ=$\frac{1}{2}$，λ+μ=1，结合①知，满足λ+μ=1的点P不唯一，⑤错误．
    综上，正确的命题是①②．
    故答案：①②．

    点评 本题考查向量加减的几何意义，涉及分类讨论以及反例的方法，是综合性题目．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    20．设平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$都是单位向量，且向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为60°，若$\overrightarrow{c}$=2x$\overrightarrow{a}$+y$\overrightarrow{b}$，其中x，y为正实数，则xy的最大值为（　　）
    A．$\frac{1}{6}$B．$\frac{1}{5}$C．$\frac{1}{4}$D．$\frac{1}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知等比数列{an}满足：a2+a3=3，a3+a4=6，那么$\sqrt{{a_4}•{a_{12}}}$=（　　）
    A．128B．81C．64D．49

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．在△ABC中，角A，B，C所对的边分别是a，b，c，且$\frac{cosA}{a}$+$\frac{cosB}{b}$=$\frac{sinC}{c}$，b2+c2-a2=$\frac{6}{5}$bc，则tanB=（　　）
    A．4B．$\frac{1}{4}$C．$\frac{6}{5}$D．$\frac{5}{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．在（x2-x+2y）5的展开式中，x4y2的系数为（　　）
    A．-120B．120C．30D．-80

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．已知△ABC中，a=$\sqrt{13}$，∠A=60°，S△=3$\sqrt{3}$，求b、c的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知三点A（2，3），B（-1，-1），C（6，k），其中k为常数．若|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|，则$\overrightarrow{AB}$与$\overrightarrow{AC}$的夹角的余弦值为0或-$\frac{24}{25}$，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．某学生家长为缴纳该学生上大学时的教育费，于2003年8月20号从银行贷款a元，为还清这笔贷款，该家长从2004年起每年的8月20号便去银行偿还确定的金额，计划恰好在贷款的m年后还清，若银行按年利息为p的复利计息（复利：即将一年后的贷款利息也纳入本金计算新的利息），则该学生家长每年的偿还金额是（　　）
    A．$\frac{a}{m}$B．$\frac{{ap{{（1+p）}^{m+1}}}}{{{{（1+p）}^{m+1}}-1}}$
    C．$\frac{{ap{{（1+p）}^{m+1}}}}{{{p^m}-1}}$D．$\frac{{ap{{（1+p）}^m}}}{{{{（1+p）}^m}-1}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞0，b＞0）$的离心率为$\frac{{\sqrt{3}}}{2}$，且焦距为4$\sqrt{3}$
    （I）求椭圆C的方程；
    （Ⅱ）设直线l：y=kx+m与椭圆C交于A、B两点，且△AOB的面积为4，其中O为坐标原点，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案