
分析 (Ⅰ)由椭圆的离心率为$\frac{{\sqrt{3}}}{2}$,且焦距为4$\sqrt{3}$,列出方程组求出a,b,由此能求出椭圆C的方程.
(Ⅱ)联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得(4k2+1)x2+8kmx+4m2-16=0,利用根的判别式、韦达定理、弦长公式,结合已知条件能求出m的取值范围.
解答 解:(Ⅰ)∵椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>0,b>0)$的离心率为$\frac{{\sqrt{3}}}{2}$,且焦距为4$\sqrt{3}$,
∴$\left\{\begin{array}{l}{\frac{c}{a}=\frac{\sqrt{3}}{2}}\\{2c=4\sqrt{3}}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a=4,b=2,
∴椭圆C的方程$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1$.
(Ⅱ)设A(x1,y1),B(x2,y2),
联立$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{16}+\frac{{y}^{2}}{4}=1}\end{array}\right.$,得(4k2+1)x2+8kmx+4m2-16=0,
由△=(8km)2-4(4k2+1)(4m2-16)>0,得m2<4+16k2,
${x}_{1}+{x}_{2}=-\frac{8km}{4{k}^{2}+1}$,${x}_{1}{x}_{2}=\frac{4{m}^{2}-16}{4{k}^{2}+1}$,
|AB|=$\sqrt{1+{k}^{2}}•\sqrt{(-\frac{8km}{4{k}^{2}+1})^{2}-\frac{4(4{m}^{2}-16)}{4{k}^{2}+1}}$=4$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{16{k}^{2}+4-{m}^{2}}}{4{k}^{2}+1}$,
∴△AOB的面积S△AOB=$\frac{1}{2}$|AB|•$\frac{|m|\sqrt{16{k}^{2}+4-{m}^{2}}}{4{k}^{2}+1}$=2$\sqrt{(4-\frac{{m}^{2}}{4{k}^{2}+1})•\frac{{m}^{2}}{4{k}^{2}+1}}$,
∴2$\sqrt{(4-\frac{{m}^{2}}{4{k}^{2}+1})•\frac{{m}^{2}}{4{k}^{2}+1}}$=4,∴m2=2(4k2+1),
由k2≥0,m2≥2,得$m≥\sqrt{2}$或m$≤-\sqrt{2}$,
∴m的取值范围为(-∞,-$\sqrt{2}$]∪[$\sqrt{2},+∞$).
点评 本题考查椭圆方程的求法,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意根的判别式、韦达定理、弦长公式、椭圆性质的合理运用.


科目:高中数学 来源: 题型:填空题
 如图四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列五个命题中正确的是①②
如图四边形ABCD是正方形,延长CD至E,使得DE=CD.若动点P从点A出发,沿正方形的边按逆时针方向运动一周回到A点,其中$\overrightarrow{AP}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AE}$,下列五个命题中正确的是①②查看答案和解析>>
科目:高中数学 来源: 题型:解答题
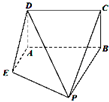 如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.
如图,已知矩形ABCD所在平面垂直于直角梯形ABPE所在平面于直线AB,平面ABCD∩平面ABPE=AB,且AB=BP=2,AD=AE=1,AE⊥AB,且AE∥BP.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (-∞,-$\frac{3\root{3}{2}}{2}$) | C. | (0,+∞) | D. | (-∞,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 12 | C. | 6 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com