
分析 (1)通过将圆C1的一般式方程化为标准方程,求出圆心与半径,利用圆心到直线的距离d=$\frac{|3k|}{\sqrt{{k}^{2}+1}}$≤2,求出k的取值范围;
(2)设当直线l的方程为y=kx,通过联立直线l与圆C1的方程,利用根的判别式大于0、韦达定理、中点坐标公式及参数方程与普通方程的相互转化,计算即得结论
解答 解:(1)∵圆C1:x2+y2-6x+5=0,
整理,得其标准方程为:(x-3)2+y2=4,
∴圆C1的圆心坐标为(3,0),半径为2,
设直线l的方程为y=kx,即kx-y=0,
∴圆心到直线的距离d=$\frac{|3k|}{\sqrt{{k}^{2}+1}}$≤2,∴-$\frac{2\sqrt{5}}{5}$≤k≤$\frac{2\sqrt{5}}{5}$;
(2)设直线l的方程为y=kx、A(x1,y1)、B(x2,y2),
与圆C1,联立方程组,消去y可得:(1+k2)x2-6x+5=0,
由△=36-4(1+k2)×5>0,可得k2<$\frac{4}{5}$.
由韦达定理,可得x1+x2=$\frac{6}{1+{k}^{2}}$,
∴线段AB的中点M的轨迹C的参数方程为$\left\{\begin{array}{l}{x=\frac{3}{1+{k}^{2}}}\\{y=\frac{3k}{1+{k}^{2}}}\end{array}\right.$,其中-$\frac{2\sqrt{5}}{5}$<k<$\frac{2\sqrt{5}}{5}$,
∴线段AB的中点M的轨迹C的方程为:(x-$\frac{3}{2}$)2+y2=$\frac{9}{4}$,其中$\frac{5}{3}$<x≤3.
点评 本题考查求圆的方程、直线与曲线的位置关系问题,注意解题方法的积累,属于中档题.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
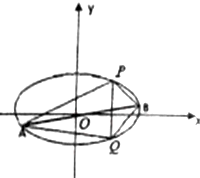 已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率为$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ∅ | B. | [-1,2] | C. | [1,2] | D. | (1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com