练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，已知△ABC为直角三角形，其中∠ACB＝90°，M为AB的中点，PM垂直于△ABC所在平面，那么(　　)

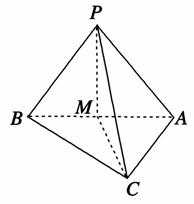
    A．PA＝PB>PC                                            B．PA＝PB<PC

    C．PA＝PB＝PC                                           D．PA≠PB≠PC


    C

    [解析]　∵M为AB的中点，△ACB为直角三角形，

    ∴BM＝AM＝CM，又PM⊥平面ABC，

    ∴Rt△PMB≌Rt△PMA≌Rt△PMC，故PA＝PB＝PC.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    如图，若Ω是长方体ABCD－A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体，其中E为线段A1B1上异于B1的点，F为线段BB1上异于B1的点，且EH∥A1D1，则下列结论中不正确的是(　　)

    A．EH∥FG

    B．四边形EFGH是矩形

    C．Ω是棱柱

    D．Ω是棱台

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两条直线m、n，两个平面α、β.给出下面四个命题：①m∥n，m⊥α⇒n⊥α；②α∥β，mα，nβ⇒m∥n；

    ③m∥n，m∥α⇒n∥α；④α∥β，m∥n，m⊥α⇒n⊥β.

    其中正确命题的序号是(　　)

    A．①③　　B．②④　　C．①④　　D．②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：


     对于直线m、l和平面α、β，α⊥β的一个充分条件是(　　)

    A．m⊥l，m∥α，l∥β　　　　                      B．m⊥l，α∩β＝m，lα

    C．m∥l，m⊥α，l⊥β                                   D．m∥l，l⊥β，mα

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，∠BAC＝90°，PC⊥平面ABC，则在△ABC，△PAC的边所在的直线中，与PC垂直的直线有________；与AP垂直的直线有________．

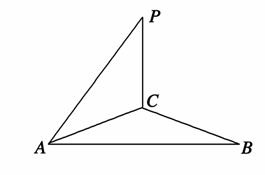
    查看答案和解析>>

    科目：高中数学 来源： 题型：


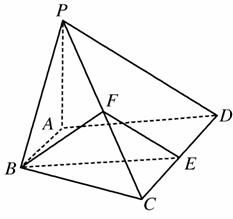
    如图，在四棱锥P－ABCD中，AB∥CD，AB⊥AD，CD＝2AB，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD、PC的中点，求证：

    (1)PA⊥底面ABCD；

    (2)BE∥平面PAD；

    (3)平面BEF⊥平面PCD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    一个几何体的三视图如图所示，该几何体从上到下由四个简单几何体组成，其体积分别记为V1，V2，V3，V4，若上面两个简单几何体均为旋转体，下面两个简单几何体均为多面体，则有：(　　)

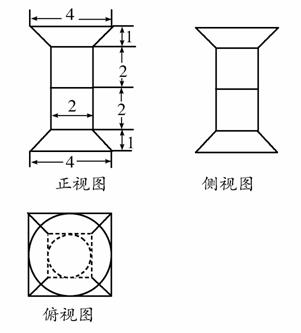
    A．V1 ＜V2＜V4 ＜V3                                   B．V1 ＜V3＜V2＜V4

    C．V2＜V1＜V3＜V4                                      D．V2＜V3 ＜V1＜V4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在空间直角坐标系中，点P(1,2,3)关于x轴对称的点的坐标为(　　)

    A．(－1,2,3)                                                  B．(1，－2，－3)

    C．(－1，－2,3)                                            D．(－1,2，－3)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如右图，若P为正方体AC1的棱A1B1的中点，则截面PC1D和面AA1B1B所成锐二面角的余弦值是____________．

    查看答案和解析>>

    同步练习册答案