
分析 (Ⅰ)求出函数的导数,通过讨论m的范围,求出函数的单调区间即可;
(Ⅱ)构造函数g(x)=emx-x,g(x)=emx-x与y=m图象两交点的横坐标为x1,x2,问题转化为证明$g({x_1})<g({\frac{-2lnm}{m}-{x_1}})$令$h(x)=g(x)-g({\frac{-2lnm}{m}-x})={e^{mx}}-2x-{e^{2lnm-mx}}-\frac{2lnm}{m}$,根据函数的单调性证明即可.
解答 解:(Ⅰ)∵f(x)=ln(x+m)-mx,∴$f'(x)=\frac{1}{x+m}-m$,
当m≤0时,∴$f'(x)=\frac{1}{x+m}-m>0$,
即f(x)的单调递增区间为(-m,+∞),无减区间;
当m>0时,∴$f'(x)=\frac{1}{x+m}-m=\frac{{-m({x+m-\frac{1}{m}})}}{x+m}$,
由f'(x)=0,得$x=\frac{1}{m}-m∈({-m,+∞})$,
$x∈({-m,-m+\frac{1}{m}})$时,f'(x)>0,
$x∈({-m+\frac{1}{m},+∞})$时,f'(x)<0,
∴m>0时,易知f(x)的单调递增区间为$({-m,-m+\frac{1}{m}})$,单调递减区间为$({-m+\frac{1}{m},+∞})$,
(Ⅱ)由(Ⅰ)知f(x)的单调递增区间为$({-m,-m+\frac{1}{m}})$,单调递减区间为$({-m+\frac{1}{m},+∞})$.
不妨设-m<x1<x2,由条件知$\left\{\begin{array}{l}ln({{x_1}+m})=m{x_1}\\ ln({{x_2}+m})=m{x_2}\end{array}\right.$,即$\left\{\begin{array}{l}{x_1}+m={e^{m{x_1}}}\\{x_2}+m={e^{m{x_2}}}\end{array}\right.$,
构造函数g(x)=emx-x,g(x)=emx-x与y=m图象两交点的横坐标为x1,x2,
由g'(x)=emx-1=0可得$x=\frac{-lnm}{m}<0$,
而m2>lnm(m>1),∴$\frac{-lnm}{m}∈({-m,+∞})$
知g(x)=emx-x在区间$({-m,\frac{-lnm}{m}})$上单调递减,在区间$({\frac{-lnm}{m},+∞})$上单调递增.
可知$-m<{x_1}<\frac{-lnm}{m}<{x_2}$
欲证x1+x2<0,只需证${x_1}+{x_2}<\frac{2lnm}{m}$,即证${x_2}<\frac{2lnm}{m}-{x_1}∈({-\frac{lnm}{m},+∞})$,
考虑到g(x)在$({\frac{-lnm}{m},+∞})$上递增,只需证$g({x_2})<g({\frac{-2lnm}{m}-{x_1}})$
由g(x2)=g(x1)知,只需证$g({x_1})<g({\frac{-2lnm}{m}-{x_1}})$
令$h(x)=g(x)-g({\frac{-2lnm}{m}-x})={e^{mx}}-2x-{e^{2lnm-mx}}-\frac{2lnm}{m}$,
则$h'(x)=m{e^{mx}}-2-({-m}){e^{-2mlnm-mx}}=m({{e^{mx}}+\frac{{{e^{-2lnm}}}}{{{e^{mx}}}}})-2≥2m\sqrt{{e^{-2lnm}}}-2=2m\sqrt{{m^{-2}}}-2=0$,
即h(x)单增,又$h({-\frac{lnm}{m}})=0$,
结合$-m<{x_1}<\frac{-lnm}{m}$知h(x1)<0,即$g({x_1})<g({\frac{-2lnm}{m}-{x_1}})$成立,
即x1+x2<0成立.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想、考查转化思想以及函数恒成立问题,是一道综合题.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:选择题
| A. | 7 | B. | 6 | C. | 9 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充要条件 | B. | 充分而不必要条件 | ||
| C. | 必要而不充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
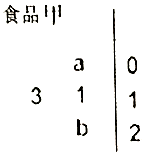 为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | 3 | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com