练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．不共线向量$\overrightarrow a$，$\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|$，且$\overrightarrow a⊥（{\overrightarrow a-2\overrightarrow b}）$，则$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$．

    分析 设$\overrightarrow a$与$\overrightarrow b$的夹角为θ，利用两个向量垂直的性质，两个向量数量积的定义，求得cosθ的值，可得θ的值．

    解答 解：设$\overrightarrow a$与$\overrightarrow b$的夹角为θ，∵不共线向量$\overrightarrow a$，$\overrightarrow b$满足$|{\overrightarrow a}|=|{\overrightarrow b}|$，且$\overrightarrow a⊥（{\overrightarrow a-2\overrightarrow b}）$，则θ∈（0，π），
    ∴$\overrightarrow{a}•$（$\overrightarrow{a}$-2$\overrightarrow{b}$）=${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$=${\overrightarrow{a}}^{2}$-2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cosθ=${\overrightarrow{a}}^{2}$-2${\overrightarrow{a}}^{2}$cosθ=0，∴cosθ=$\frac{1}{2}$，∴θ=$\frac{π}{3}$，
    故答案为：$\frac{π}{3}$．

    点评 本题主要考查两个向量垂直的性质，两个向量数量积的定义，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    7．已知函数f（x）=x3+2ax2+1在x=1处的切线的斜率为1，则实数a=$-\frac{1}{2}$，此时函数y=f（x）在[0，1]最小值为$\frac{23}{27}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．已知函数f（x）=$\frac{{x}^{2}+2x}{{e}^{x}}$，f′（x）为f（x）的导函数，则f′（0）的值为2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．在△ABC中，角A，B，C所对的边分别为a，b，c，且满足$\sqrt{3}$cos2A+1=4sin（$\frac{π}{6}$+A）•sin（$\frac{π}{3}$-A）
    （Ⅰ）求角A的值；
    （Ⅱ）若a=$\sqrt{2}$，且b≥a，求$\sqrt{2}$b-c的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知函数f（x）=|2x-a|-|x-1|．
    （1）当a=1时，求f（x）的最小值；
    （2）存在x∈[0，2]时，使得不等式f（x）≤0成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知f（x）=ln（x+m）-mx．
    （Ⅰ）求f（x）的单调区间；
    （Ⅱ）设m＞1，x1，x2为函数f（x）的两个零点，求证：x1+x2＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    9．某几何体的三视图如图，则该几何体的体积是（　　）
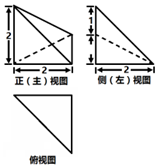
    A．4B．$\frac{4}{3}$C．$\frac{8}{3}$D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知抛物线y=ax2+2x-a-1（a∈R），恒过第三象限上一定点A，且点A在直线3mx+ny+1=0（m＞0，n＞0）上，则$\frac{1}{m}+\frac{1}{n}$的最小值为（　　）
    A．4B．12C．24D．36

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知正项数列{an}的前n项和为Sn，且2Sn=（an-1）（an+2）．
    （1）求证：不论λ取何值，数列{an+λan+1}总是等差数列，并求此数列的公差；
    （2）设数列$\{\frac{{（n-1）•{2^n}}}{{n{a_n}}}\}$的前n项和为Tn，试比较Tn与$\frac{{{2^{n+1}}（18-n）-2n-2}}{n+1}$的大小．

    查看答案和解析>>

    同步练习册答案