
| A. | 4 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | 2 |
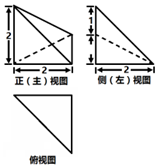
分析 根据三视图,得直观图是三棱锥,底面积为$\frac{1}{2}×2×2\sqrt{2}$=2$\sqrt{2}$,高为$\sqrt{2}$,即可求出它的体积.
解答 解:根据三视图,得直观图是三棱锥,底面积为$\frac{1}{2}×2×2\sqrt{2}$=2$\sqrt{2}$,高为$\sqrt{2}$;
所以,该棱锥的体积为V=$\frac{1}{3}$S底面积•h=$\frac{1}{3}$×2$\sqrt{2}×\sqrt{2}$=$\frac{4}{3}$.
故选:B.
点评 本题考查了利用三视图求体积的应用问题,解题的关键是根据三视图得出几何体的结构特征,是基础题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | e | B. | 2 | C. | 1 | D. | $\frac{e}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
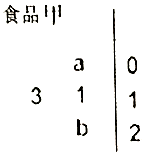 为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )
为保障春节期间的食品安全,某市质量监督局对超市进行食品检查,如图所示是某品牌食品中微量元素含量数据的茎叶图,已知该组数据的平均数为11.75,则$\frac{4}{a}+\frac{1}{b}$的最小值为( )| A. | 9 | B. | $\frac{9}{2}$ | C. | 3 | D. | $\frac{7}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com