
【题目】将![]() 方格表任意一个角上的
方格表任意一个角上的![]() 小方格表挖去,剩下的图形称为“角形”.现在
小方格表挖去,剩下的图形称为“角形”.现在![]() 方格表中放置一些两两不重叠的角形,要求角形的边界与方格表的边界或分格线重合.求正整数
方格表中放置一些两两不重叠的角形,要求角形的边界与方格表的边界或分格线重合.求正整数![]() 的最大值,使得无论以何种方式放置了
的最大值,使得无论以何种方式放置了![]() 个角形之后,总能在方格表中再放入一个完整的角形.
个角形之后,总能在方格表中再放入一个完整的角形.
【答案】5
【解析】
首先,![]() .这是因为,若按下图的方式放置6个角形,则不能再于此方格表中放入另一个完整的角形.
.这是因为,若按下图的方式放置6个角形,则不能再于此方格表中放入另一个完整的角形.

现按任意方式放置5个角形.
接下来证明此时仍可再放入一个完整的角形.
考虑下图中的五个阴影区域![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .若存在某块区域与所放的5个角形均不交,则显然可在该区域内放人一个完整的角形.
.若存在某块区域与所放的5个角形均不交,则显然可在该区域内放人一个完整的角形.

下设五个区域均含角形或角形的一部分.注意到,一个角形不可能与![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中的两个区域同时相交.故五个区域
中的两个区域同时相交.故五个区域![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 各对应一个与之相交的角形,这5个角形中没有重复的,将它们分别记为
各对应一个与之相交的角形,这5个角形中没有重复的,将它们分别记为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .
.
按图的方式,将![]() 方格表四个角上的
方格表四个角上的![]() 小方格表区域分别记为
小方格表区域分别记为![]() 、
、![]() 、
、![]() 、
、![]() .
.
注意到,角形![]() 不可能同时与四个区域口
不可能同时与四个区域口![]() 、
、![]() 、
、![]() 、
、![]() 相交,不妨设
相交,不妨设![]() 与
与![]() 不交.考虑到角形
不交.考虑到角形![]() 、
、![]() 、
、![]() 也与
也与![]() 不交,故与口相交的角形只有
不交,故与口相交的角形只有![]() 这一个.然而,区域口被角形
这一个.然而,区域口被角形![]() 所占的部分必包含于
所占的部分必包含于![]() 的某个角上的
的某个角上的![]() 小方格表中,不失一般性,设包含在图阴影区域中,则可以如图所示在
小方格表中,不失一般性,设包含在图阴影区域中,则可以如图所示在![]() 的剩余部分放置一个新的角形.
的剩余部分放置一个新的角形.

以上表明![]() 符合题意.
符合题意.
综上,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地,目前德国汉堡,美国波士顿等申办城市因市民担心赛事费用超支而相继退出,某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运有关?
(3)已知在被调查的年龄大于50岁的支持者中有6名女性,其中2名是女教师.现从这6名女性中随机抽取2名,求恰有1名女教师的概率.
附: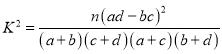 ,
,![]() ,
,
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若函数
,若函数![]() 是增函数,则称函数
是增函数,则称函数![]() 具有性质A.
具有性质A.
![]() 若
若![]() ,求
,求![]() 的解析式,并判断
的解析式,并判断![]() 是否具有性质A;
是否具有性质A;
![]() 判断命题“减函数不具有性质A”是否真命题,并说明理由;
判断命题“减函数不具有性质A”是否真命题,并说明理由;
![]() 若函数
若函数![]() 具有性质A,求实数k的取值范围,并讨论此时函数
具有性质A,求实数k的取值范围,并讨论此时函数![]() 在区间
在区间![]() 上零点的个数.
上零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两队进行篮球决赛,采取五场三胜制(当一队赢得三场胜利时,该队获胜,比赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主”.设甲队主场取胜的概率为![]() ,客场取胜的概率为
,客场取胜的概率为![]() ,且各场比赛结果相互独立,则甲队不超过
,且各场比赛结果相互独立,则甲队不超过![]() 场即获胜的概率是( )
场即获胜的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第七届世界军人运动会于2019年10月18日至27日在中国武汉举行,中国队以133金64银42铜位居金牌榜和奖牌榜的首位.运动会期间有甲、乙等五名志愿者被分配到射击、田径、篮球、游泳四个运动场地提供服务,要求每个人都要被派出去提供服务,且每个场地都要有志愿者服务,则甲和乙恰好在同一组的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二年级共有800名学生参加了数学测验(满分150分),已知这800名学生的数学成绩均不低于90分,将这800名学生的数学成绩分组如:![]() ,
,![]() ,
,![]() ,
,![]() ,
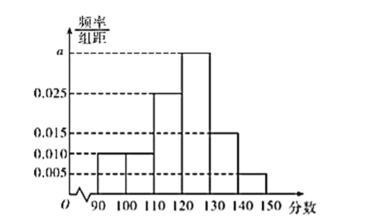
,![]() ,得到的频率分布直方图如图所示,则下列说法中正确的是( )
,得到的频率分布直方图如图所示,则下列说法中正确的是( )
①![]() ;②这800名学生中数学成绩在110分以下的人数为160; ③这800名学生数学成绩的中位数约为121.4;④这800名学生数学成绩的平均数为125.
;②这800名学生中数学成绩在110分以下的人数为160; ③这800名学生数学成绩的中位数约为121.4;④这800名学生数学成绩的平均数为125.
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着“中华好诗词”节目的播出,掀起了全民诵读传统诗词经典的热潮.某社团为调查大学生对于“中华诗词”的喜好,从甲、乙两所大学各随机抽取了40名学生,记录他们每天学习“中华诗词”的时间,并整理得到如下频率分布直方图:

根据学生每天学习“中华诗词”的时间,可以将学生对于“中华诗词”的喜好程度分为三个等级 :
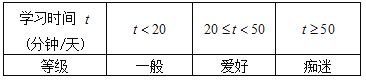
(Ⅰ)从甲大学中随机选出一名学生,试估计其“爱好”中华诗词的概率;
(Ⅱ)从两组“痴迷”的同学中随机选出2人,记![]() 为选出的两人中甲大学的人数,求
为选出的两人中甲大学的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() ;
;
(Ⅲ)试判断选出的这两组学生每天学习“中华诗词”时间的平均值![]() 与
与![]() 的大小,及方差
的大小,及方差![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com