
分析 求出数列的等比与首项,化简a1a2…an,然后求解最值.
解答 解:等比数列{an}满足a1+a3=10,a2+a4=5,
可得q(a1+a3)=5,解得q=$\frac{1}{2}$.
a1+q2a1=10,解得a1=8.
则a1a2…an=a1n•q1+2+3+…+(n-1)=8n•$(\frac{1}{2})^{\frac{n(n-1)}{2}}$=${2}^{3n-\frac{{n}^{2}-n}{2}}$=${2}^{\frac{7n-{n}^{2}}{2}}$,
当n=3或4时,表达式取得最大值:${2}^{\frac{12}{2}}$=26=64.
故答案为:64.
点评 本题考查数列的性质数列与函数相结合的应用,转化思想的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
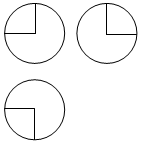 如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )
如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是$\frac{28π}{3}$,则它的表面积是( )| A. | 17π | B. | 18π | C. | 20π | D. | 28π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
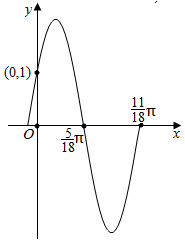
| A. | $\sqrt{3}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com