
分析 (1)先设出函数关系式,代入速度与每小时燃料费的关系值求出比例系数即可;
(2)根据题设要求设出行驶总费用与速度之间的函数关系式,再利用函数的导数去求函数的最小值即可.
解答 解:(1)设能源费用每小时是w千元,车速是vkm/h,依题意有w=kv3(k为比例系数),
将v=100,w=0.06代入得k=6×10-8.于是有w=6×10-8v3.
因此列车从甲地行驶到乙地,所需的总费用为y=$\frac{1750}{v}$(w+3.24)=1750(6×10-8v2+$\frac{3.24}{v}$),(0<v≤C)(C为常数,0<C≤400).
(2)由(1)化简得y=105(10-6v2+$\frac{54}{v}$),
设f(x)=10-6x2+$\frac{54}{x}$,x>0,
所以f′(x)=2×10-6x-$\frac{54}{{x}^{2}}$,
当f′(x)>0时,解得x>300,当f′(x)<0时,解得0<x<300,
所以0<C<300,函数在(0,C]上单调递减,v=C时,运行全程所需的总费用最低;
300≤C≤400时,v=300,运行全程所需的总费用最低.
点评 本题是实际应用题,考查学生建立函数模型的能力,以及利用函数的导数研究给定区间上函数的最值问题,是高考的常考知识点.


科目:高中数学 来源: 题型:解答题
 某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有320人,为调查高一年级学生每天晚自习自主支配学习时间(指除了完成老师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 15 | C. | 18 | D. | 不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4\overrightarrow{OP}$ | B. | $3\overrightarrow{OP}$ | C. | $2\overrightarrow{OP}$ | D. | $\overrightarrow{OP}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
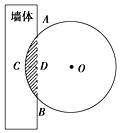 《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)| A. | 600立方寸 | B. | 610立方寸 | C. | 620立方寸 | D. | 633立方寸 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com