
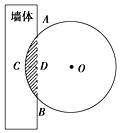
 《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)| A. | 600立方寸 | B. | 610立方寸 | C. | 620立方寸 | D. | 633立方寸 |
分析 由题意画出图形,求出圆柱的底面半径,进一步求出弓形面积,代入体积公式得答案.
解答 解:如图,
AB=10(寸),则AD=5(寸),CD=1(寸),
设圆O的半径为x(寸),则OD=(x-1)(寸),
在Rt△ADO中,由勾股定理可得:52+(x-1)2=x2,解得:x=13(寸).
∴sin∠AOD=$\frac{AD}{AO}=\frac{5}{13}$,即∠AOD≈22.5°,则∠AOB=45°.
则弓形$\widehat{ACB}$的面积S=$\frac{1}{2}×\frac{π}{4}×1{3}^{2}-\frac{1}{2}×10×12$≈6.33(平方寸).
则算该木材镶嵌在墙中的体积约为V=6.33×100=633(立方寸).
故选:D.
点评 本题考查棱柱、棱锥、棱台体积的求法,关键是对题意的理解,是中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (4,+∞) | B. | $[3+2\sqrt{2}\;\;,\;\;+∞)$ | C. | [6,+∞) | D. | $(4\;\;,\;\;3+2\sqrt{2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:
某制造商为运动会生产一批直径为40mm的乒乓球,现随机抽样检查20只,测得每只球的直径(单位:mm,保留两位小数)如下:| 40.02 | 40.00 | 39.98 | 40.00 | 39.99 |
| 40.00 | 39.98 | 40.01 | 39.98 | 39.99 |
| 40.00 | 39.99 | 39.95 | 40.01 | 40.02 |
| 39.98 | 40.00 | 39.99 | 40.00 | 39.96 |
| 分组 | 频数 | 频率 | $\frac{频率}{组距}$ |
| [39.95,39.97) | 2 | ||
| [39.97,39.99) | 4 | ||
| [39.99,40.01) | 10 | ||
| [40.01,40.03] | 4 | ||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
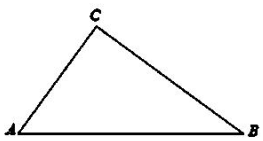 如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com