
| A. | 13 | B. | 15 | C. | 18 | D. | 不确定 |
分析 由已知可求最大角的值,设三边长为x,x+2,x+4,利用余弦定理即可解得边长,从而可求周长.
解答 解:∵最大角的余弦值为$\frac{{\sqrt{3}}}{2}$,则最大角为$\frac{2}{3}π$($\frac{π}{3}$不满足三角形),
不妨设三边长为x,x+2,x+4,
则由余弦定理可得:$cos\frac{2π}{3}=\frac{{{x^2}+{{(x+2)}^2}-{{(x+4)}^2}}}{2x(x+2)}⇒{x_1}=3,{x_2}=-2$(舍),
故周长为3+5+7=15.
故选:B.
点评 本题主要考查了余弦定理在解三角形中的应用,考查了计算能力和转化思想,属于基础题.


 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{9}$+$\frac{y^2}{5}$=1(y≠0) | B. | $\frac{y^2}{9}$+$\frac{x^2}{5}$=1(x≠0) | C. | $\frac{x^2}{9}$+$\frac{y^2}{5}$=1(x≠3) | D. | $\frac{y^2}{9}$+$\frac{x^2}{5}$=1(y≠3) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 减少3.5个单位 | B. | 增加2个单位 | C. | 增加3.5个单位 | D. | 减少2个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
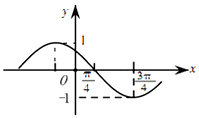
| A. | $y=sin(x+\frac{π}{4})$ | B. | $y=sin(2x+\frac{3π}{4})$ | C. | $y=cos(x+\frac{π}{4})$ | D. | $y=cos(2x+\frac{3π}{4})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com