
| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
分析 (1)求出回归系数,即可求y关于x的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$;
(2)x=12时,$\widehat{y}$=-0.56×12+12.92=6.2,即可预测该店明天的营业额;
(3)X~N(7,10),P(0.6<X<10.2)=P(0.6<X<7)+P(7<X<10.2)=
解答 解:(1)根据题意,计算$\overline x=\frac{1}{5}×(2+5+8+9+11)=7$,$\overline y=\frac{1}{5}×(12+10+8+8+7)=9$,…(2分)
$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x^2}_i-n{{\overline x}^2}}}}=\frac{287-5×7×9}{295-5×7×7}=-0.56$,…(4分)
$\hat a=\overline y-\hat b\overline x=9-(-0.56)×7=12.92$,
∴y关于x的回归直线方程$\widehat{y}$=-0.56x+12.92; …(6分)
(2)x=12时,$\widehat{y}$=-0.56×12+12.92=6.2,
预测该店明天的营业额为6200元; …(8分)
(3)由题意,平均数为μ=7,方差为σ2=10,
所以X~N(7,10),…(10分)
所以P(0.6<X<10.2)=P(0.6<X<7)+P(7<X<10.2)=$\frac{1}{2}×0.9545+\frac{1}{2}×0.6827=0.8186$. …(12分)
点评 本题考查了回归直线方程和正态分布的应用问题,是综合题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [4,+∞) | C. | [2$\sqrt{3}$,+∞) | D. | [4$\sqrt{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
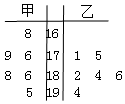 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com