
| A. | [2,+∞) | B. | [4,+∞) | C. | [2$\sqrt{3}$,+∞) | D. | [4$\sqrt{3}$,+∞) |
分析 利用三角形的面积公式和椭圆的性质得出a≥4,再根据三角形的面积公式得出当A与短轴端点重合时,c取得最小值,利用椭圆的性质求出2c的最小值即可.
解答 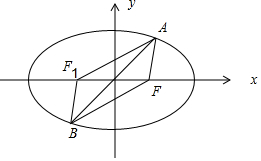 解:取椭圆的左焦点F1,连接AF1,BF1,
解:取椭圆的左焦点F1,连接AF1,BF1,
则AB与FF1互相平分,
∴四边形AFBF1是平行四边形,
∴AF1=BF,
∵AF+AF1=2a,∴AF+BF=2a,
∵S△ABF=$\frac{1}{2}$AF•BF•sin120°=$\frac{\sqrt{3}}{4}$AF•BF=4$\sqrt{3}$,
∴AF•BF=16,
∵2a=AF+BF≥2$\sqrt{AF•BF}$=8,∴a≥4,
又S△ABF=$\frac{1}{2}×c×2|{y}_{A}|$=c•|yA|=4$\sqrt{3}$,
∴c=$\frac{4\sqrt{3}}{|{y}_{A}|}$,
∴当|yA|=b=$\sqrt{{a}^{2}-{c}^{2}}$时,c取得最小值,此时b=$\sqrt{3}$c,
∴a2=3c2+c2=4c2,∴2c=a,
∴2c≥4.
故选B.
点评 本题考查了椭圆的性质,直线与椭圆的位置关系,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{8}{5}$ | B. | $\frac{9}{5}$ | C. | $-\frac{9}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | 2 | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 5 | 8 | 9 | 11 |
| y | 12 | 10 | 8 | 8 | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 21 | B. | -21 | C. | 441 | D. | -441 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com