
分析 数列{an}满足a1=2,an+1=$\frac{2(n+2)}{n+1}$an(n∈N*),可得$\frac{{a}_{n+1}}{n+2}$=2•$\frac{{a}_{n}}{n+1}$,$\frac{{a}_{1}}{1+1}$=1.利用等比数列的通项公式可得:an=(n+1)•2n-1.再利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:∵数列{an}满足a1=2,an+1=$\frac{2(n+2)}{n+1}$an(n∈N*),
∴$\frac{{a}_{n+1}}{n+2}$=2•$\frac{{a}_{n}}{n+1}$,$\frac{{a}_{1}}{1+1}$=1.
∴$\frac{{a}_{n}}{n+1}$=2n-1,即an=(n+1)•2n-1.
设其前n项和为Sn,则Sn=2+3×2+4×22+…+(n+1)•2n-1.
∴2Sn=2×2+3×22+…+n•2n-1+(n+1)•2n.
∴-Sn=2+2+22+…+2n-1-(n+1)•2n=1+$\frac{{2}^{n}-1}{2-1}$-(n+1)•2n.
∴Sn=n•2n.
则$\frac{{a}_{2017}}{{a}_{1}+{a}_{2}+…+{a}_{2016}}$=$\frac{2018×{2}^{2016}}{2016×{2}^{2016}}$=$\frac{1009}{1008}$.
故答案为:$\frac{1009}{1008}$.
点评 本题考查了“错位相减法”、等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | [4,+∞) | C. | [2$\sqrt{3}$,+∞) | D. | [4$\sqrt{3}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
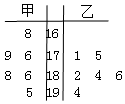 在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:
在一次水稻试验田验收活动中,将甲、乙两种水稻随机抽取各6株样品,单株籽粒数制成如图所示的茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )
已知抛物线x2=2py和$\frac{{x}^{2}}{2}$-y2=1的公切线PQ(P是PQ与抛物线的切点,未必是PQ与双曲线的切点)与抛物线的准线交于Q,F(0,$\frac{P}{2}$),若$\sqrt{2}$|PQ|=$\sqrt{3}$|PF|,则抛物线的方程是( )| A. | x2=4y | B. | x2=2$\sqrt{3}$y | C. | x2=6y | D. | x2=2$\sqrt{2}$y |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<1} | B. | {x|-1<x<2} | C. | {x|0<x<2} | D. | {x|-1<x<1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com