Question

2．已知圆C：x²+y²+2x-8y+m=0与抛物线上E：y²=8x的准线l相切，抛物线E上的点P到准线l的距离为d，Q为圆C上任意一点，则|PQ|+d的最小值等于（　　）

• A． 3
• B． 2
• C． 4
• D． 5

Answer 1

分析 圆C：x²+y²+2x-8y+m=0与抛物线上E：y²=8x的准线l相切，求出圆心与半径，抛物线y²=8x的准线为l：x=-2，焦点为F（2，0），当P，Q，F三点共线时，P到点Q的距离d与点P到抛物线的焦点距离|PQ|之和最小，从而d+|PQ|的最小值为|FC|-r．

解答 解：圆C：x²+y²+2x-8y+m=0配方，得（x+1）²+（y-4）²=17-m，圆心为C（-1，4），半径r=$\sqrt{17-m}$．
∵圆C与抛物线上E：y²=8x的准线l相切，∴$\sqrt{17-m}$=1，∴m=16
如图所示，由题意，知抛物线y²=8x的焦点为F（2，0），连接PF，则d=|PF|．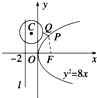
d+|PQ|=|PF|+|PQ|，显然，|PF|+|PQ|≥|FQ|（当且仅当F，P，Q三点共线时取等号）．
而|FQ|为圆C上的动点Q到定点F的距离，
显然当F，Q，C三点共线时取得最小值，
最小值为|CF|-r=$\sqrt{（-1-2）^{2}+（4-0）^{2}}$-1=5-1=4．
故选：C．

点评 本题考查线段和的最小值的求法，考查抛物线的定义，是中档题，正确转化是关键．