
(本题满分12分)设过点 的直线分别与
的直线分别与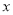 轴和
轴和 轴交于
轴交于 两点,点
两点,点 与点
与点 关于
关于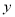 轴对称,
轴对称,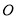 为坐标原点,若
为坐标原点,若 且
且 .
.
(Ⅰ)求点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)过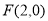 的直线与轨迹
的直线与轨迹 交于
交于 两点,求
两点,求 的取值范围.
的取值范围.
(Ⅰ)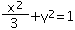 ;(Ⅱ)(
;(Ⅱ)( ,1].
,1].
【解析】
试题分析:(Ⅰ)求动点的轨迹方程的一般步骤:1.建系——建立适当的坐标系.2.设点——设轨迹上的任一点P(x,y).3.列式——列出动点P所满足的关系式.4.代换——依条件式的特点,选用距离公式、斜率公式等将其转化为x,y的方程式,并化简.5.证明——证明所求方程即为符合条件的动点的轨迹方程.
(Ⅱ)与圆锥曲线相关的最值、范围问题综合性较强,解决的思路有两种:一是由题目中的限制条件求范围,如直线与圆锥曲线的位置关系中Δ的范围,方程中变量的范围,角度的大小等;二是将要讨论的几何量如长度、面积、代数式等用参数表示出来,再对表达式进行讨论,应用不等式、三角函数等知识求最值,在解题过程中注意向量,不等式的应用.
试题解析:(1)∵过点P(x,y)的直线分别与x轴和y轴交于A,B两点,点Q与点P关于y轴对称,∴Q(-x,y),设A(a, 0),B(0,b),
∵O为坐标原点,∴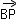 =(x,y-b),
=(x,y-b),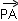 =(a-x,-y),
=(a-x,-y),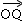 =(-x,y),
=(-x,y),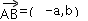 ,
,
∵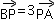 且
且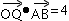 ,
,
∴ ,
,
解得点P的轨迹M的方程为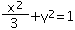 .
.
(2)设过F(2,0)的直线方程为y=kx-2k,
联立 ,得(3k2+1)x2-12k2x+12k2-3=0,
,得(3k2+1)x2-12k2x+12k2-3=0,
设A(x1,y1),B(x2,y2),则x1+x2=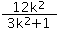 ,x1x2=
,x1x2=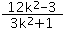 ,
,
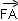 =(x1-2,y1),
=(x1-2,y1),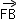 =(x2-2,y2),
=(x2-2,y2),
∴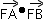 =(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2)=(1+k2)[x1x2-2(x1+x2)+4]
=(x1-2)(x2-2)+y1y2=(1+k2)(x1-2)(x2-2)=(1+k2)[x1x2-2(x1+x2)+4]
=(1+k2)(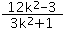 -
-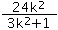 +4)=
+4)=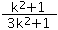 =
= +
+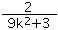 ,
,
∴当k2→∞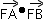 的最小值→
的最小值→ ;当k=0时,
;当k=0时,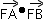 的最大值为1.
的最大值为1.
∴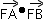 的取值范围是(
的取值范围是( ,1].
,1].
考点:轨迹方程、圆锥曲线中的范围、最值问题


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测理科数学试卷(解析版) 题型:选择题
设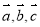 是非零向量,已知命题p:若
是非零向量,已知命题p:若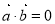 ,
,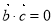 ,则
,则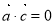 ;命题q:若
;命题q:若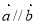 ,
,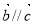 ,则
,则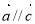 . 则下列命题中真命题是
. 则下列命题中真命题是
A. B.
B.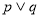 C.
C.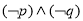 D.
D.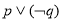
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省四地六校高三上学期第三次月考理科数学试卷(解析版) 题型:选择题
如图,正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,
M为棱BB1的中点,则下列结论中错误的是( )
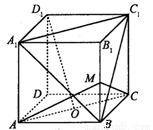
A.D1O∥平面A1BC1
B.D1O⊥平面AMC
C.异面直线BC1与AC所成的角等于60°
D.二面角M-AC-B等于45°
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省绥化市三校高二上学期期中联考数学试卷(解析版) 题型:填空题
设点 是椭圆
是椭圆 与圆
与圆 的一个交点,
的一个交点,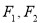 分别
分别
是椭圆的左、右焦点,且 ,则椭圆的离心率为 .
,则椭圆的离心率为 .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年黑龙江省绥化市三校高二上学期期中联考数学试卷(解析版) 题型:选择题
一个圆的圆心为椭圆的右焦点F,且该圆过椭圆的中心交椭圆于点P, 直线PF (F
(F 为椭圆的左焦点)是该圆的切线,则椭圆的离心率为( )
为椭圆的左焦点)是该圆的切线,则椭圆的离心率为( )
A. B.
B. C.
C. D.
D.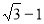
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com