
| A. | 4 | B. | 8 | C. | 10 | D. | 13 |
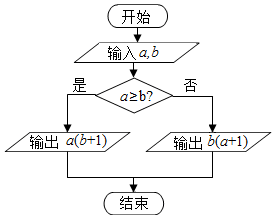
分析 根据程序框图可得,当a≥b时,则输出a(b+1),反之,则输出b(a+1),比较2tan$\frac{13π}{4}$与lg$\frac{1}{10}$,lne与($\frac{1}{5}$)-1的大小,即可求解得到答案.
解答 解:模拟执行程序,可得,当a≥b时,则输出a(b+1),反之,则输出b(a+1),
∵2tan$\frac{13π}{4}$=2,lg$\frac{1}{10}$=-1,
∴(2tan$\frac{13π}{4}$)?lg$\frac{1}{10}$=(2tan$\frac{13π}{4}$)×(lg$\frac{1}{10}$+1)=2×(-1+1)=0,
∵lne=1,($\frac{1}{5}$)-1=5,
∴lne?($\frac{1}{5}$)-1=($\frac{1}{5}$)-1×(lne+1)=5×(1+1)=10,
∴[(2tan$\frac{13π}{4}$)?lg$\frac{1}{10}$]+[lne?($\frac{1}{5}$)-1]=0+10=10.
故选:C.
点评 本题考查了程序框图,对应的知识点是条件结构的应用,其中正确理解各变量的含义并根据程序功能的需要合理的分析是解答的关键.属于基础题.


 应用题作业本系列答案
应用题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | 26,12,12 | B. | 25,13,12 | C. | 25,12,13 | D. | 24,13,13 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com