
分析 (Ⅰ)由sin2θ+cos2θ=1,可得圆C的普通方程,再由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,即可得到圆的极坐标方程;
(Ⅱ)由于圆经过原点,由圆的极坐标方程,代入$θ=\frac{π}{12}$,计算即可得到弦长.
解答 解:(Ⅰ)由sin2θ+cos2θ=1,可得
圆C的普通方程是(x-$\frac{\sqrt{2}}{2}$)2+(y-$\frac{\sqrt{2}}{2}$)2=1,
由x=ρcosθ,y=ρsinθ,x2+y2=ρ2,
又x2+y2-$\sqrt{2}$x$-\sqrt{2}y$=0,即有ρ2=$\sqrt{2}$ρ(cosθ+sinθ),
即有圆的极坐标方程是ρ=2cos(θ-$\frac{π}{4}$);
(Ⅱ)由圆的极坐标方程可得,
当$θ=\frac{π}{12}$时,
ρ=2cos($\frac{π}{12}$-$\frac{π}{4}$)=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
故|AB|=$\sqrt{3}$.
点评 本题考查参数方程和普通方程及极坐标方程的互化,同时考查极坐标方程的运用,属于基础题.


科目:高中数学 来源: 题型:解答题
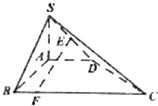 在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.
在四棱锥S-ABCD中,SA⊥平面ABCD,∠BAD=∠ABC=90°,SA=AB=AD=$\frac{1}{3}$BC=1,E为SD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2) | B. | [0,2] | C. | {0,1,2} | D. | {0,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2] | B. | ∅ | C. | [-4,-1] | D. | [-4,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{4}{3}$) | B. | ($\frac{1}{2}$,$\frac{4}{3}$) | C. | (1,$\frac{7}{4}$) | D. | ($\frac{1}{2}$,$\frac{7}{4}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com