
已知a,b,m,n均为正数,且a+b=1,mn=2,则(am+bn)(bm+an)的最小值为________.
2
[解析] 解法1:∵a,b,m,n∈R+,且a+b=1,mn=2,
∴(am+bn)(an+bm)=abm2+a2mn+b2mn+abn2
=ab(m2+n2)+2(a2+b2)≥2abmn+2(a2+b2)
=4ab+2(a2+b2)=2(a+b)2=2,
当且仅当m=n=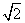 时,取等号,
时,取等号,
∴所求最小值为2.
解法2:由柯西不等式(a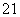 +a
+a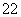 +…+a
+…+a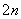 )(b
)(b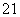 +b
+b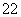 +…+b
+…+b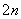 )≥(a1b1+a2b2+…+anbn)2,等号成立时,bi=0(i=1,2,…,n)或存在实数k,使得ai=kbi(i=1,2,…,n),及a,b,m,n∈R+,a+b=1,mn=2,得
)≥(a1b1+a2b2+…+anbn)2,等号成立时,bi=0(i=1,2,…,n)或存在实数k,使得ai=kbi(i=1,2,…,n),及a,b,m,n∈R+,a+b=1,mn=2,得
(am+bn)(an+bm)≥(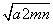 +
+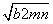 )2
)2
=(a+b)2·mn=2,等号在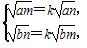 时成立,
时成立,
∴k=1,m=n=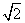 时,(am+bn)(an+bm)取到最小值2.
时,(am+bn)(an+bm)取到最小值2.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
设n为正整数,f(n)=1+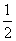 +
+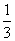 +…+
+…+ ,计算得f(2)=
,计算得f(2)=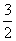 ,f(4)>2,f(8)>
,f(4)>2,f(8)>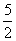 ,f(16)>3,观察上述结论,可推测一般的结论为________.
,f(16)>3,观察上述结论,可推测一般的结论为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
如图,直线AB为圆的切线,切点为B,点C在圆上,∠ABC的角平分线BE交圆于点E,DB垂直BE交圆于点D.
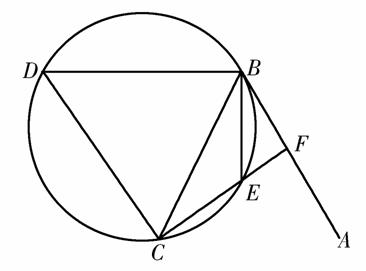
(1)证明:DB=DC;
(2)设圆的半径为1,BC=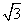 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知曲线C1的参数方程为
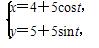 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sinθ.
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).
查看答案和解析>>
科目:高中数学 来源: 题型:
椭圆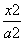 +
+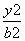 =1(a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为________.
=1(a>b>0)的左、右顶点分别是A,B,左、右焦点分别是F1,F2.若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com