练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝|x－2|－|x－5|.

    (1)证明：－3≤f(x)≤3；

    (2)求不等式f(x)≥x2－8x＋15的解集．


    　(1)f(x)＝|x－2|－|x－5|

    ＝

    当2<x<5时，－3<2x－7<3.

    所以－3≤f(x)≤3.

    (2)由(1)可知，

    当x≤2时，f(x)≥x2－8x＋15的解集为空集；

    当2<x<5时，f(x)≥x2－8x＋15的解集为{x|5－≤x<5}；

    当x≥5时，f(x)≥x2－8x＋15的解集为{x|5≤x≤6}．

    综上，不等式f(x)≥x2－8x＋15的解集为{x|5－≤x≤6}．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    观察下列事实：|x|＋|y|＝1的不同整数解(x，y)的个数为4 , |x|＋|y|＝2的不同整数解(x，y)的个数为8, |x|＋|y|＝3的不同整数解(x，y)的个数为12，…，则|x|＋|y|＝20的不同整数解(x，y)的个数为(　　)

    A．76                                                           B．80

    C．86                                                           D．92

    查看答案和解析>>

    科目：高中数学 来源： 题型：


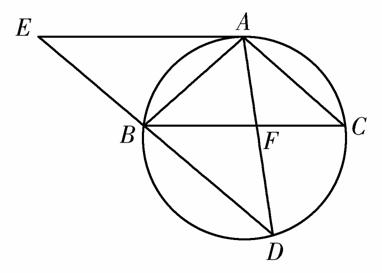
    如图，△ABC为圆的内接三角形，BD为圆的弦，且BD∥AC.过点A作圆的切线与DB的延长线交于点E，AD与BC交于点F.若AB＝AC，AE＝6，BD＝5，则线段CF的长为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    曲线C的直角坐标方程为x2＋y2－2x＝0，以原点为极点，x轴的正半轴为极轴建立极坐标系，则曲线C的极坐标方程为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设集合A＝{x||x－a|<1，x∈R}，B＝{x||x－b|>2，x∈R}．若A⊆B，则实数a，b必满足(　　)

    A．|a＋b|≤3                                                 B．|a＋b|≥3

    C．|a－b|≤3                                                 D．|a－b|≥3

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a，b，m，n均为正数，且a＋b＝1，mn＝2，则(am＋bn)(bm＋an)的最小值为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知两点M(－2,0)，N(2,0)，点P满足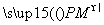·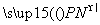＝0，则点P的轨迹方程为(　　)

    A.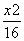＋y2＝1                                                B．x2＋y2＝4

    C．y2－x2＝8                                                 D．x2＋y2＝8

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如果双曲线－＝1上一点P到它的右焦点的距离是8，那么点P到它的左焦点的距离是(　　)

    A．4                                                             B．12

    C．4或12                                                      D．不确定

    查看答案和解析>>

    同步练习册答案