
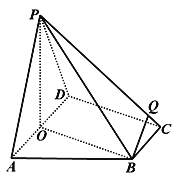
【题目】如图,四棱锥中![]() ,底面
,底面![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,平面
,平面![]() 底面
底面![]() ,
,![]() ,
,![]() .
.

(Ⅰ)判断平面![]() 与平面
与平面![]() 是否垂直,并给出证明;
是否垂直,并给出证明;
(Ⅱ)若![]() ,
,![]() ,
,![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)见证明;(Ⅱ)![]()
【解析】
(Ⅰ)利用反证法证明,假设面PBC⊥面PCD,过点B作BQ⊥PC于Q,由面面垂直的性质可得BQ⊥CD,知BC⊥CD,则CD⊥PC,由平面![]() 底面
底面![]() ,则CD⊥PD,出现矛盾;(Ⅱ)取AD中点O,连PO,OB,证明OA、OB、OP两两互相垂直,以OA、OB、OP所在直线分别为x、y、z轴建立如空间直角坐标系O﹣xyz,分别求面PAB与面PBC的法向量,由两法向量所成角余弦值可得二面角A﹣PB﹣C余弦值.
,则CD⊥PD,出现矛盾;(Ⅱ)取AD中点O,连PO,OB,证明OA、OB、OP两两互相垂直,以OA、OB、OP所在直线分别为x、y、z轴建立如空间直角坐标系O﹣xyz,分别求面PAB与面PBC的法向量,由两法向量所成角余弦值可得二面角A﹣PB﹣C余弦值.
(Ⅰ)平面![]() 与平面
与平面![]() 不垂直.证明如下:
不垂直.证明如下:
假设平面![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 于
于![]()
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
∴![]() 平面
平面![]()
∴![]()
在直角梯形![]() 中,由
中,由![]() ,
,![]() 知
知![]()
又∵![]()
∴ ![]() 平面
平面![]() ,故
,故![]()
∵ 平面![]() 底面
底面![]() ,平面
,平面![]() 底面
底面![]() ,
,![]()
∴ ![]() 平面
平面![]() ∴
∴ ![]()
![]()
在![]() 中,不可能有两个直角,所以假设不成立
中,不可能有两个直角,所以假设不成立
(Ⅱ)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]()
∵![]() ∴
∴![]()
∵ 平面![]() 底面
底面![]() ,平面
,平面![]() 底面
底面![]()
∴![]() 底面
底面![]()
∵在直角梯形![]() 中,
中,![]() ,
,![]() ∴
∴![]()
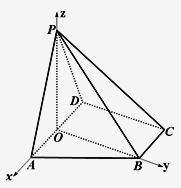
以![]() 、
、![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 、
、![]() 轴建立如图所示空间直角坐标系
轴建立如图所示空间直角坐标系![]()
∵![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,![]()
∴![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]()
由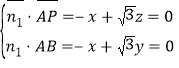 , 取
, 取![]()
同理可得平面![]() 的法向量
的法向量![]()
∴ .
.
由图形可知,所求二面角为钝角
∴二面角![]() 的余弦值
的余弦值![]()


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点F(1,0),O为坐标原点,A,B是抛物线C上异于 O的两点.
的焦点F(1,0),O为坐标原点,A,B是抛物线C上异于 O的两点.
(1)求抛物线C的方程;
(2)若直线AB过点(8,0),求证:直线OA,OB的斜率之积为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别相交于
分别相交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在圆心在原点的定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位组织“学习强国”知识竞赛,选手从6道备选题中随机抽取3道题.规定至少答对其中的2道题才能晋级.甲选手只能答对其中的4道题。
(1)求甲选手能晋级的概率;
(2)若乙选手每题能答对的概率都是![]() ,且每题答对与否互不影响,用数学期望分析比较甲、乙两选手的答题水平。
,且每题答对与否互不影响,用数学期望分析比较甲、乙两选手的答题水平。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知直线
中,已知直线![]() :
: (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的直角坐标为
的直角坐标为![]() ,直线
,直线![]() 与曲线
与曲线![]() 的交点为
的交点为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年全国数学奥赛试行改革:在高二一年中举行5次全区竞赛,学生如果其中2次成绩达全区前20名即可进入省队培训,不用参加其余的竞赛,而每个学生最多也只能参加5次竞赛.规定:若前4次竞赛成绩都没有达全区前20名,则第5次不能参加竞赛.假设某学生每次成绩达全区前20名的概率都是![]() ,每次竞赛成绩达全区前20名与否互相独立.
,每次竞赛成绩达全区前20名与否互相独立.
(1)求该学生进入省队的概率.
(2)如果该学生进入省队或参加完5次竞赛就结束,记该学生参加竞赛的次数为![]() ,求
,求![]() 的分布列及
的分布列及![]() 的数学期望.
的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() 和⊙
和⊙![]()
![]() ,过抛线
,过抛线![]() 上一点
上一点![]() 作两条直线与⊙
作两条直线与⊙![]() 相切于A、B两点,分别交抛物线于E、F两点,圆心点
相切于A、B两点,分别交抛物线于E、F两点,圆心点![]() 到抛物线准线的距离为
到抛物线准线的距离为![]() .
.
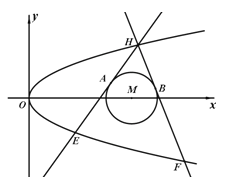
(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)当![]() 的角平分线垂直x轴时,求直线EF的斜率;
的角平分线垂直x轴时,求直线EF的斜率;
(Ⅲ)若直线AB在![]() 轴上的截距为
轴上的截距为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com