
 如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.
如图,△BCD与△MCD都是边长为2的正三角形,平面MCD⊥平面BCD,AB⊥平面BCD,AB=2$\sqrt{3}$.分析 (Ⅰ)取CD中点O,连OB,OM,证明MO⊥平面BCD,推出MO∥AB,延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角,推出求解三角形求解直线AM与平面BCD所成角的大小为45°;
(Ⅱ)利用等体积法VA-BDM=VM-ABD求解即可.
(III)CE是平面ACM与平面BCD的交线.由(I)知,O是BE的中点,则BCED是菱形,作BF⊥EC于F,连AF,则AF⊥EC,∠AFB就是二面角A-EC-B的平面角,设为,通过求解三角形求解二面角的正弦值.
解答 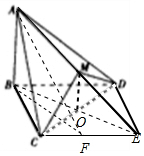 (14分)解:(Ⅰ)取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,
(14分)解:(Ⅰ)取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,
又平面MCD⊥平面BCD,则MO⊥平面BCD,
所以MO∥AB,
A、B、O、M共面,
延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角,
OB=MO=$\sqrt{3}$,MO∥AB,则$\frac{EO}{EB}=\frac{MO}{AB}$=$\frac{1}{2}$,EO=OB=$\sqrt{3}$,
所以EB=2$\sqrt{3}$=AB,即∠AEB=45°.
∴直线AM与平面BCD所成角的大小为45°;
(Ⅱ)△BCD与△MCD都是边长为2的正三角形,
VA-BDM=VM-ABD=VO-ABD=$\frac{1}{3}×\frac{1}{2}×AB•BD•\frac{1}{2}×\frac{\sqrt{3}}{2}BD$=1;
( III)CE是平面ACM与平面BCD的交线.
由(I)知,O是BE的中点,则BCED是菱形,
作BF⊥EC于F,连AF,则AF⊥EC,
∠AFB就是二面角A-EC-B的平面角,设为θ,
因为∠BCE=120°,
所以∠BCF=60°,
BF=BCcos60$°=\sqrt{3}$,tanθ=$\frac{AB}{BF}$=2,sinθ=$\frac{2\sqrt{5}}{5}$.
所以,所求二面角的正弦值是$\frac{2\sqrt{5}}{5}$.
点评 本题考查直线与平面市场价,二面角的平面角的求法,几何体的体积的求法,考查计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | b<a<c | C. | c<b<a | D. | b<c<a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
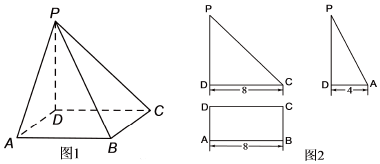
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | a<c<b | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{2\sqrt{5}}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
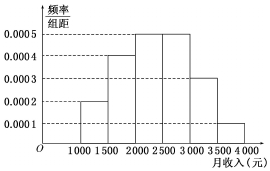 某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).
某市统计局就本地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示月收入在[1000,1500)(单位:元)).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com