
 如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB∥ED,且ED=FB=1,G为BC的中点.
如图,四边形ABCD是边长为1的正方形,ED⊥平面ABCD,FB∥ED,且ED=FB=1,G为BC的中点.分析 (1)可把几何体补成一个边长为1的正方体ABCD-MFNE,则此几何体的体积:V=13-VA-MEF-VC-NEF,由此能求出结果.
(2)以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,由此能求出在线段AF上存在点P,使得GP⊥平面AEF,并能求出线段AP的长.
(3)求出平面AEF的一个法向量,平面BAF的法向量,利用向量法能求出二面角E-AF-B的余弦值.
解答 解:(1)如图,可把几何体补成一个边长为1的正方体ABCD-MFNE,
∴此几何体的体积:
V=13-VA-MEF-VC-NEF
=1-$\frac{1}{3}×(\frac{1}{2}×1×1)×1$-$\frac{1}{3}×(\frac{1}{2}×1×1)×1$
=$\frac{2}{3}$.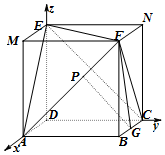 (2)如图,以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,
(2)如图,以D为原点,DA为x轴,DC为y轴,DE为z轴,建立空间直角坐标系,
则A(1,0,0),G($\frac{1}{2}$,1,0),E(0,0,1),F(1,1,1),
∴$\overrightarrow{AF}$=(0,1,1),$\overrightarrow{EF}$=(1,1,0),$\overrightarrow{AG}$=(-$\frac{1}{2}$,1,0),
设$\overrightarrow{AP}$=$λ\overrightarrow{AF}$=(0,λ,λ),则$\overrightarrow{GP}$=$\overrightarrow{AP}-\overrightarrow{AG}$=($\frac{1}{2},λ-1,λ$),
由$\overrightarrow{GP}$⊥$\overrightarrow{AF}$,得$\overrightarrow{GP}•\overrightarrow{AF}$=λ-1+λ=0,
解得$λ=\frac{1}{2}$,
此时$\overrightarrow{GP}$=($\frac{1}{2},-\frac{1}{2}$,$\frac{1}{2}$),$\overrightarrow{GP}$$•\overrightarrow{EF}$=0,
∴此时GP⊥平面AEF,
线段AP的长|AP|=$\sqrt{{0}^{2}+(\frac{1}{2})^{2}+(\frac{1}{2})^{2}}$=$\frac{\sqrt{2}}{2}$.
(3)由(2)知平面AEF的一个法向量$\overrightarrow{GP}$=($\frac{1}{2},-\frac{1}{2},\frac{1}{2}$),
平面BAF的法向量$\overrightarrow{n}$=(1,0,0),
cod<$\overrightarrow{GP}$,$\overrightarrow{n}$>=$\frac{\overrightarrow{GP}•\overrightarrow{n}}{|\overrightarrow{GP}|•|\overrightarrow{n}|}$=$\frac{\frac{1}{2}}{\sqrt{\frac{3}{4}}}$=$\frac{\sqrt{3}}{3}$,
由图知二面角E-AF-B的平面角是钝角,
∴二面角E-AF-B的余弦值为-$\frac{\sqrt{3}}{3}$.
点评 本题考查几何体体积的求法,考查满足条件的点是否存在的判断与求法,二查二面角的余弦值的求法,涉及到空间中线线、线面、面面间的位置关系等知识点,考查推理论证能力、运算求解能力、数据处理能力,考查化归与转化思想、函数与方程思想、数形结合思想,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | n>m>p | B. | p>m>n | C. | m>n>p | D. | m>p>n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
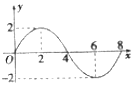 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,x≥0)的部分图象如图所示,则f(1)+f(2)+f(3)+…+f(11)的值等于( )| A. | 2 | B. | $2+\sqrt{2}$ | C. | $2+2\sqrt{2}$ | D. | $-2-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|-3<x<0} | B. | {x|-3<x<3} | C. | {x|0<x<2} | D. | {x|0<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{28}$ | B. | $\frac{3}{8}$ | C. | $\frac{3}{7}$ | D. | $\frac{2}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 一次购物量 | 1至4件 | 5至8件 | 9至12件 | 13至16件 | 17件及以上 |
| 顾客数(人) | x | 30 | 25 | y | 10 |
| 结算时间(分钟/人) | 1 | 1.5 | 2 | 2.5 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com