
分析 (1)求导数,利用函数f(x)=a•lnx+b•x2的图象在点(1,f(1))处的切线方程为x-y-1=0,求出a,b,即可求f(x)的表达式;
(2)由题要证函数g(x)=2f(x+t),t∈R且t≤2,是函数h(x)=ex+f(x+t)的一个“游离承托函数”,只要证明当t≤2时,g(x)<h(x)在公共定义域上恒成立.
解答 (1)解:当x=1时,y=0,代入f(x)=a•lnx+b•x2得b=0,…(1分)
所以f(x)=a•lnx,f′(x)=$\frac{a}{x}$…(3分)
由切线方程知f′(1)=1,所以a=1,故f(x)=lnx.…(5分)
(2)证明:由题要证函数g(x)=2f(x+t),t∈R且t≤2,是函数h(x)=ex+f(x+t)的一个“游离承托函数”,
只要证明当t≤2时,g(x)<h(x)在公共定义域上恒成立,即证明:
当t≤2时,h(x)-g(x)=ex-ln(x+t)对于x>-t恒成立,
由于t≤2,x+t≤x+2,ln(x+t)≤ln(x+2),ex-ln(x+t)≥ex-ln(x+2),
只要证明:ex-ln(x+2)>0对于x>-2恒成立即可.…(6分)
证明:令y=ex-ln(x+2),x>-2,
则y′=ex-$\frac{1}{x+2}$,
令k(x)=ex-$\frac{1}{x+2}$,则k′(x)=ex+$\frac{1}{(x+2)^{2}}$>0,
∴y′=ex-$\frac{1}{x+2}$在(-2,+∞)上单调递增,且k(-1)=$\frac{1}{e}$-1<0,k(0)=1-$\frac{1}{2}$>0
∴?x0∈(-1,0),使得k(x0)=0成立,…(8分)
当x∈(-2,x0)时,y′<0,y=ex-ln(x+2)单调递减;
当x∈(x0,+∞)时,y′>0,y=ex-ln(x+2)单调递增;
∴ymin=${e}^{{x}_{0}}$-ln(x0+2),…(9分)
又由k(x0)=0,得${e}^{{x}_{0}}$=$\frac{1}{{x}_{0}+2}$,且x0=-ln(x0+2)…(10分)
∴ymin=${e}^{{x}_{0}}$-ln(x0+2)=$\frac{({x}_{0}+1)^{2}}{{x}_{0}+2}$>0,…(11分)
∴ex-ln(x+2)>0对于x>-2恒成立
∴函数函数g(x)=2f(x+t),t∈R且t≤2,是函数h(x)=ex+f(x+t)的一个“游离承托函数”,得证.…(12分)
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及函数恒成立问题等基础题知识,考查运算求解能力,考查化归与转化思想,分类讨论思想,属于难题.


科目:高中数学 来源: 题型:解答题
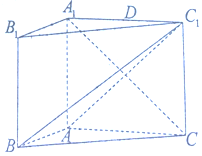 如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C
如图,在三棱柱ABC-A1B1C1中,侧面ABB1A1是矩形,∠BAC=90°,AA1⊥BC,AA1=AC=2AB=4,且BC1⊥A1C查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{\sqrt{5}}{5}$ | C. | -$\sqrt{5}$ | D. | -$\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x与g(x)=($\sqrt{x}$)2 | B. | f(x)=x|x|与g(x)=$\left\{\begin{array}{l}{{x}^{2}(x>0)}\\{-{x}^{2}(x<0)}\end{array}\right.$ | ||
| C. | f(x)=|x|与g(x)=$\root{3}{{x}^{3}}$ | D. | f(x)=$\frac{{x}^{2}-1}{x-1}$与g(t)=t+1(t≠1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com