
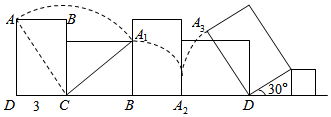
分析 由弧长、面积公式分别求出各段弧长、面积,相加即可求解.
解答 解:第一面翻滚时,点A的路程为$\overline{A{A}_{1}}$,其圆心角为$\frac{π}{2}$,半径为5 dm,
所走过的弧长为$\frac{5}{2}$π dm,所在的扇形的面积为$\frac{25}{4}$π dm2.
第二面翻滚时,点A的路程为$\overline{{A}_{1}{A}_{2}}$,其圆心角为$\frac{π}{2}$,半径为3 dm,
所走过的弧长为$\frac{3}{2}$π dm,所在的扇形的面积为$\frac{9}{4}$π dm2.
第三面翻滚时,点A(图中的点A2)在桌面上不动;
第四面翻滚时,点A的路为$\overline{{A}_{2}{A}_{3}}$,其圆心角为$\frac{π}{2}$-$\frac{π}{6}$=$\frac{π}{3}$,半径为4 dm,
所走过的路程为$\frac{4}{3}$π dm,所在扇形的面积为$\frac{8}{3}$π dm2,
所以总路程为$\frac{5}{2}$π+$\frac{3}{2}$π+$\frac{4}{3}$π=$\frac{16}{3}$π(dm).
走过的弧所在的扇形总面积为$\frac{25}{4}$π+$\frac{9}{4}$π+$\frac{4}{3}$π=$\frac{59}{6}$π(dm2).
点评 本题考查弧长、面积公式,求出各段弧长的半径和圆心角是解题的关键,有一定的难度.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
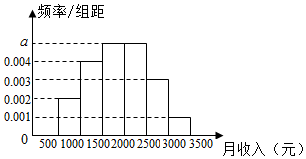 统计局就某地居民的月收入情况调查了10000人,并根据所得数据画出了样本频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[500,1000)元.
统计局就某地居民的月收入情况调查了10000人,并根据所得数据画出了样本频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在[500,1000)元.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
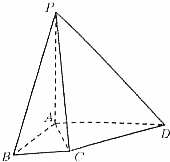 如图,四棱锥P-ABCD中,PA⊥平面ABCD,BC∥AD,∠BAD=120°,AP=AB=AD=2BC.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,BC∥AD,∠BAD=120°,AP=AB=AD=2BC.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com