Question

3．如图：正三棱柱ABC-A₁B₁C₁中，D是BC的中点，AA₁=AB=1．
（1）求证：A₁C∥平面AB₁D；
（2）求点C到平面AB₁D的距离．
（3）求二面角B-AB₁-D的大小．

Answer 1

分析 （1）如图，在正三棱柱中，易证明E是A₁B的中点，又D是BC的中点，故得DE∥A₁C，从而通过线面平行的判定定理可得结论；
（2）根据面面垂直的性质和判定定理，易得CH的长度就是点C到平面ABCD的距离，再通过相似三角形的性质可得结论；
（3）二面角的度量关键在于找出它的平面角，构造平面角常用的方法就是三垂线法．在面ABC内作DF⊥AB于点F，由平面A₁ABB₁⊥平面ABC可知：DF⊥平面A₁ABB₁，从而∠FGD是二面角B-AB₁-D的平面角，计算即可．

解答 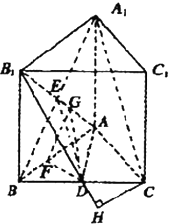（1）证明：连接A₁B，设A₁B∩AB₁=E，连结DE，
∵ABC-A₁B₁C₁是正三棱柱且AA₁=AB，
∴四边形A₁ABB₁是正方形，∴E是A₁B的中点，
又D是BC的中点，∴DE∥A₁C，
∵DE?平面AB₁D，A₁C?平面AB₁D，∴A₁C∥平面AB₁D；
（2）解：∵平面B₁BC₁⊥平面ABC，且AD⊥BC，∴AD⊥平面B₁BCC₁，
又AD?平面AB₁D，∴平面B₁BCC₁⊥平面AB₁D，
在平面B₁BCC₁内作CH⊥B₁D交B₁D的延长线于点H，
则CH的长度就是点C到平面ABCD的距离，
由△CDH∽△B₁DB得：$CH=\frac{{B{B_1}•CD}}{{{B_1}D}}=\frac{{\sqrt{5}}}{5}$，
即点C到平面AB₁D的距离是$\frac{{\sqrt{5}}}{5}$；
（3）解：在平面ABC内作DF⊥AB于点F，在平面A₁ABB₁内作FG⊥AB₁于点G，连结DG．
∵平面A₁ABB₁⊥平面ABC，∴DF⊥平面A₁ABB₁，FG是DG在平面A₁ABB₁上的射影，
∵FG⊥AB₁，∴DG⊥AB₁，∴∠FGD是二面角B-AB₁-D的平面角，
∵A₁A=AB=1，在正△ABC中，$DF=\frac{{\sqrt{3}}}{4}$，在△ABE中，FG=$\frac{3}{4}BE=\frac{{3\sqrt{2}}}{8}$，
在Rt△DFG中，$tan∠FGD=\frac{DF}{FG}=\frac{{\sqrt{6}}}{3}$，
∴二面角B-AB₁-D的大小为arctan$\frac{{\sqrt{6}}}{3}$．

点评 本小题主要考查空间线面关系、点到面的距离、二面角的度量等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力，属于难题．