
已知函数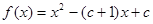
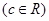 .
.
(1)解关于x的不等式f(x)<0;
(2)当c=-2时,不等式f(x)>ax-5在 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;
(1)当c<1时,不等式的解集为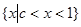 ,当c=1时,不等式的解集为
,当c=1时,不等式的解集为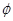 ,当c>1时,不等式的解集为
,当c>1时,不等式的解集为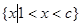 。 ;(2)a<1+2
。 ;(2)a<1+2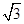
解析试题分析:(1)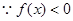
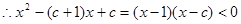 1分
1分
①当c<1时, 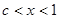
②当c=1时,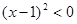 ,
,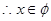
③当c>1时,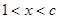 4分
4分
综上,当c<1时,不等式的解集为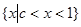 ,当c=1时,不等式的解集为
,当c=1时,不等式的解集为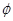 ,当c>1时,不等式的解集为
,当c>1时,不等式的解集为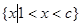 。 5分
。 5分
(2)当c=-2时,f(x)>ax-5化为x2+x-2>ax-5  ax<x2+x+3,x∈(0,2) 恒成立
ax<x2+x+3,x∈(0,2) 恒成立
∴a<(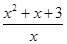 )min 设
)min 设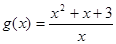 8分
8分
∴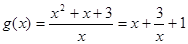 ≥1+2
≥1+2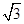 10分
10分
当且仅当x=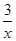 ,即x=
,即x=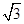 ∈(0,2)时,等号成立
∈(0,2)时,等号成立
∴g(x)min=(1+x+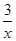 )min=1+2
)min=1+2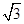
∴ a<1+2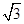 12分
12分
考点:本题考查了不等式的解法及恒成立问题的解法
点评:恒成立问题在解题过程中大致可分为以下几种类型:
①一次函数型;②二次函数型;③变量分离型;④根据函数的奇偶性、周期性等性质;⑤直接根据函数的图象。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
已知方程x2+y2-2(m+3)x+2(1-4m2) y+16m4+9=0表示一个圆,(1)求实数m取值范围;(2)求圆半径r取值范围;(3)求圆心轨迹方程。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数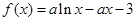 (a∈R且
(a∈R且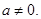 ).
).
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意t∈[1,2],函数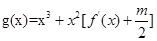 在区间(t,3)上总不是单调函数,求m的取值范围.
在区间(t,3)上总不是单调函数,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数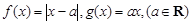 .
.
(1)判断函数 的奇偶性;(4分)
的奇偶性;(4分)
(2)若关于 的方程
的方程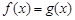 有两解,求实数
有两解,求实数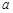 的取值范围;(6分)
的取值范围;(6分)
(3)若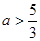 ,记
,记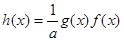 ,试求函数
,试求函数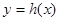 在区间
在区间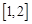 上的最大值.(10分)
上的最大值.(10分)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分) 已知函数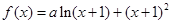 在
在 处有极值.
处有极值.
(Ⅰ)求实数 值;
值;
(Ⅱ)求函数 的单调区间;
的单调区间;
(Ⅲ)试问是否存在实数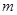 ,使得不等式
,使得不等式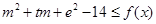 对任意
对任意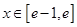 及
及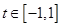
恒成立?若存在,求出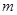 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com