
已知函数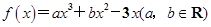 在点
在点 处的切线方程为
处的切线方程为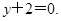
(1)求函数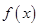 的解析式;
的解析式;
(2)若对于区间[-2,2]上任意两个自变量的值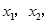 都有
都有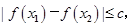 求实数c的最小值.
求实数c的最小值.
(1) f(x)=x3-3x. (2) c的最小值为4.
解析试题分析:(1)f′(x)=3ax2+2bx-3.
根据题意,得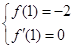
即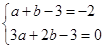 解得
解得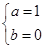
所以f(x)=x3-3x.
(2)令f′(x)=0,即3x2-3=0,得x=±1.
因为f(-1)=2,f(1)=-2,x -2 (-2,-1) -1 (-1,1) 1 (1,2) 2 f′(x) + - + f(x) -2  ?
?极大值  ?
?极小值  ?
?2
所以当x∈[-2,2]时,f(x)max=2,f(x)min=-2.
( 需列表格或者说明单调性,否则扣2分)
则对于区间[-2,2]上任意两个自变量的值x1,x2,都有|f(x1)-f(x2)|≤|f(x)max-f(x)min|=4,
所以c≥4.即c的最小值为4.
考点:本题主要考查导数的几何意义,应用导数研究函数的单调性、最值,待定系数法。
点评:典型题,本题属于导数应用中的基本问题,首先利用待定系数法,求得函数解析式,为进一步解题奠定了基础。利用“表解法”写出函数单调性、极值,直观明了。


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com