
(本小题满分12分)已知函数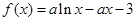 (a∈R且
(a∈R且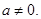 ).
).
(1)求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意t∈[1,2],函数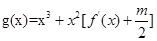 在区间(t,3)上总不是单调函数,求m的取值范围.
在区间(t,3)上总不是单调函数,求m的取值范围.
(1) 当a>0时,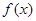 的单调增区间为(0,1),单调减区间为(1,+∞)
的单调增区间为(0,1),单调减区间为(1,+∞)
当a<0时,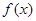 的单调增区间为(1,+∞),单调减区间为(0,1)
的单调增区间为(1,+∞),单调减区间为(0,1)
(2)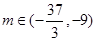
解析试题分析:解:(本小题满分12分)
(1)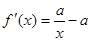 =
=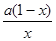 . ∵x>0, ………………………1分
. ∵x>0, ………………………1分
当a>0时,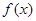 的单调增区间为(0,1),单调减区间为(1,+∞)……………2分
的单调增区间为(0,1),单调减区间为(1,+∞)……………2分
当a<0时,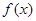 的单调增区间为(1,+∞),单调减区间为(0,1).……………4分
的单调增区间为(1,+∞),单调减区间为(0,1).……………4分
(2)∵函数y=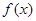 在点(2,
在点(2,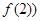 处的切线斜率为1,
处的切线斜率为1,
∴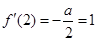 , 解得a=-2.………………………………5分
, 解得a=-2.………………………………5分
∴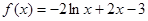 , ∴
, ∴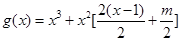
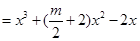 .
.
∴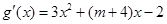 .……………………………7分
.……………………………7分
令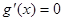 ,即
,即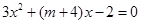 , ∵△=
, ∵△=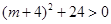 ,
,
∴方程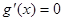 有两个实根且两根一正一负,即有且只有一个正根.…………8分
有两个实根且两根一正一负,即有且只有一个正根.…………8分
∵函数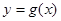 在区间(t,3)(其中t∈[1,2])上总不是单调函数,
在区间(t,3)(其中t∈[1,2])上总不是单调函数,
∴方程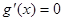 在
在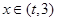 上有且只有一个实数根.………………………9分
上有且只有一个实数根.………………………9分
又∵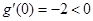 ,∴
,∴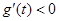 ,
,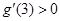 .
.
∴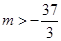 ,且
,且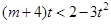 .…………………………………………10分
.…………………………………………10分
∵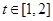 ,∴
,∴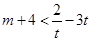 ,
,
令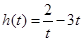 ,则
,则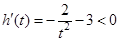 ,即
,即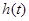 在
在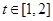 上单调递减.
上单调递减.
∴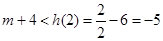 ,即
,即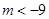 .
.
∴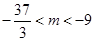 .
.
综上可得,m的取值范围为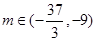 .…………………………………12分
.…………………………………12分
考点:本试题考查了导数的运用
点评:解决该试题的关键是能理解对于导数的符号,运用分类讨论的思想来求解函数的单调性。同时对于函数不单调的处理,可以转换为函数单调时的参数的范围,然后利用补集的思想求解结论,属于中档题。


科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知函数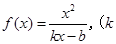 ,
,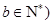 ,满足
,满足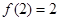 ,
,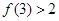 .
.
(1)求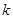 ,
,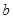 的值;
的值;
(2)若各项为正的数列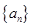 的前
的前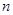 项和为
项和为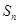 ,且有
,且有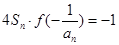 ,设
,设 ,求数列
,求数列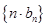 的前
的前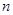 项和
项和 ;
;
(3)在(2)的条件下,证明: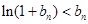 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数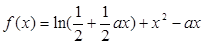
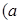 为常数,
为常数,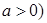
(1)当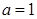 时,求函数
时,求函数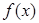 在
在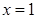 处的切线方程;
处的切线方程;
(2)当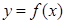 在
在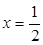 处取得极值时,若关于
处取得极值时,若关于 的方程
的方程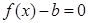 在
在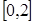 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数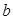 的取值范围;
的取值范围;
(3)若对任意的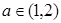 ,总存在
,总存在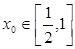 ,使不等式
,使不等式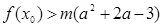 成立,求实数
成立,求实数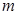 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
某种产品投放市场以来,通过市场调查,销量t(单位:吨)与利润Q(单位:万元)的变化关系如右表,现给出三种函数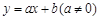 ,
,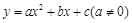 ,
,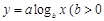 且
且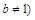 ,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
| 销量t | 1 | 4 | 6 |
| 利润Q | 2 | 5 | 4.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com